Quantum computing

Quantum is getting hot in 2019, and even Ciro Santilli got a bit excited: quantum computing could be the next big thing.

No useful algorithm has been economically accelerated by quantum yet as of 2019, only useless ones, but the bets are on, big time.

To get a feeling of this, just have a look at the insane number of startups that are already developing quantum algorithms for hardware that doesn't/barely exists! quantumcomputingreport.com/players/privatestartup (archive). Some feared we might be in a bubble: Are we in a quantum computing bubble?

To get a basic idea of what programming a quantum computer looks like start by reading: Section "Quantum computing is just matrix multiplication".

Some people have their doubts, and that is not unreasonable, it might truly not work out. We could be on the verge of an AI winter of quantum computing. But Ciro Santilli feels that it is genuinely impossible to tell as of 2020 if something will work out or not. We really just have to try it out and see. There must have been skeptics before every single next big thing.

Table of contents 12k 252

Introduction to quantum computing

Words: 41

Course plan:

Section "Programmer's model of quantum computers"
look at a Qiskit hello world
- e.g. ours: qiskit/hello.py
learn about quantum circuits.
- tensor product in quantum computing
- First we learn some quantum logic gates. This shows an alternative, and extremely important view of a quantum computer besides a matrix multiplication: as a circuit. Fundamental subsections:
- quantum algorithms
  - Section "Quantum Fourier transform"
  - Section "Shor's algorithm"

Programmer's model of quantum computers (How to program a quantum computer, Quantum computing is just matrix multiplication)

Words: 1k

This is a quick tutorial on how a quantum computer programmer thinks about how a quantum computer works. If you know:

what a complex number is
how to do matrix multiplication
what is a probability

a concrete and precise hello world operation can be understood in 30 minutes.

Although there are several types of quantum computer under development, there exists a single high level model that represents what most of those computers can do, and we are going to explain that model here. This model is the is the digital quantum computer model, which uses a quantum circuit, that is made up of many quantum gates.

Beyond that basic model, programmers only may have to consider the imperfections of their hardware, but the starting point will almost always be this basic model, and tooling that automates mapping the high level model to real hardware considering those imperfections (i.e. quantum compilers) is already getting better and better.

The way quantum programmers think about a quantum computer in order to program can be described as follows:

the input of a N qubit quantum computer is a vector of dimension N containing classic bits 0 and 1
the quantum program, also known as circuit, is a $2^{n} \times 2^{n}$ unitary matrix of complex numbers $Q \in C^{2^{n}} \times C^{2^{n}}$ that operates on the input to generate the output
the output of a N qubit computer is also a vector of dimension N containing classic bits 0 and 1

To operate a quantum computer, you follow the step of operation of a quantum computer:

set the input qubits to classic input bits (state initialization)
press a big red "RUN" button
read the classic output bits (readout)

Each time you do this, you are literally conducting a physical experiment of the specific physical implementation of the computer:

setup your physical system to represent the classical 0/1 inputs
let the state evolve for long enough
measure the classical output back out

and each run as the above can is simply called "an experiment" or "a measurement".

The output comes out "instantly" in the sense that it is physically impossible to observe any intermediate state of the system, i.e. there are no clocks like in classical computers, further discussion at: quantum circuits vs classical circuits. Setting up, running the experiment and taking the does take some time however, and this is important because you have to run the same experiment multiple times because results are probabilistic as mentioned below.

Unlike in a classical computer, the output of a quantum computer is not deterministic however.

But the each output is not equally likely either, otherwise the computer would be useless except as random number generator!

This is because the probabilities of each output for a given input depends on the program (unitary matrix) it went through.

Therefore, what we have to do is to design the quantum circuit in a way that the right or better answers will come out more likely than the bad answers.

We then calculate the error bound for our circuit based on its design, and then determine how many times we have to run the experiment to reach the desired accuracy.

The probability of each output of a quantum computer is derived from the input and the circuit as follows.

First we take the classic input vector of dimension N of 0's and 1's and convert it to a "quantum state vector"

q_{in}

of dimension

2^{n}

q_{in} \in C^{2^{n}}

(1)

We are after all going to multiply it by the program matrix, as you would expect, and that has dimension

2^{n} \times 2^{n}

Note that this initial transformation also transforms the discrete zeroes and ones into complex numbers.

For example, in a 3 qubit computer, the quantum state vector has dimension

2^{3} = 8

and the following shows all 8 possible conversions from the classic input to the quantum state vector:

000 -> 1000 0000 == (1.0, 0.0, 0.0, 0.0,  0.0, 0.0, 0.0, 0.0)
001 -> 0100 0000 == (0.0, 1.0, 0.0, 0.0,  0.0, 0.0, 0.0, 0.0)
010 -> 0010 0000 == (0.0, 0.0, 1.0, 0.0,  0.0, 0.0, 0.0, 0.0)
011 -> 0001 0000 == (0.0, 0.0, 0.0, 1.0,  0.0, 0.0, 0.0, 0.0)
100 -> 0000 1000 == (0.0, 0.0, 0.0, 0.0,  1.0, 0.0, 0.0, 0.0)
101 -> 0000 0100 == (0.0, 0.0, 0.0, 0.0,  0.0, 1.0, 0.0, 0.0)
110 -> 0000 0010 == (0.0, 0.0, 0.0, 0.0,  0.0, 0.0, 1.0, 0.0)
111 -> 0000 0001 == (0.0, 0.0, 0.0, 0.0,  0.0, 0.0, 0.0, 1.0)

This can be intuitively interpreted as:

if the classic input is 000, then we are certain that all three bits are 0.
Therefore, the probability of all three 0's is 1.0, and all other possible combinations have 0 probability.
if the classic input is 001, then we are certain that bit one and two are 0, and bit three is 1. The probability of that is 1.0, and all others are zero.
and so on

Now that we finally have our quantum state vector, we just multiply it by the unitary matrix

Q

of the quantum circuit, and obtain the

2^{n}

dimensional output quantum state vector

q_{o u t}

q_{o u t} = Q q_{in}

(2)

And at long last, the probability of each classical outcome of the measurement is proportional to the square of the length of each entry in the quantum vector, analogously to what is done in the Schrödinger equation.

For example, suppose that the 3 qubit output were:

q_{o u t} = \frac{3}{2} 0.0 \frac{1}{2} 0.0 0.0 0.0 0.0 0.0

(3)

Then, the probability of each possible outcomes would be the length of each component squared:

P (000) P (001) P (010) P (011) P (100) P (101) P (110) P (111) = \frac{3}{2}^{2} = ∣ 0 ∣^{2} = \frac{1}{2}^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = \frac{3}{2}^{2} = 0^{2} = \frac{1}{2}^{2} = 0^{2} = 0^{2} = 0^{2} = 0^{2} = 0^{2} = \frac{3}{4} = 0 = \frac{1}{4} = 0 = 0 = 0 = 0 = 0

(4)

i.e. 75% for the first, and 25% for the third outcomes, where just like for the input:

first outcome means 000: all output bits are zero
third outcome means 010: the first and third bits are zero, but the second one is 1

All other outcomes have probability 0 and cannot occur, e.g.: 001 is impossible.

Keep in mind that the quantum state vector can also contain complex numbers because we are doing quantum mechanics, but we just take their magnitude in that case, e.g. the following quantum state would lead to the same probabilities as the previous one:

\frac{1 + 2 i}{2}^{2} \frac{i}{2}^{2} = \frac{1 ^{2} + 2 ^{2}}{2 ^{2}} = \frac{1 ^{2}}{2 ^{2}} = \frac{3}{4} = \frac{1}{4}

(5)

This interpretation of the quantum state vector clarifies a few things:

the input quantum state is just a simple state where we are certain of the value of each classic input bit
the matrix has to be unitary because the total probability of all possible outcomes must be 1.0
This is true for the input matrix, and unitary matrices have the probability of maintaining that property after multiplication.
Unitary matrices are a bit analogous to self-adjoint operators in general quantum mechanics (self-adjoint in finite dimensions implies is stronger)
This also allows us to understand intuitively why quantum computers may be capable of accelerating certain algorithms exponentially: that is because the quantum computer is able to quickly do an unitary matrix multiplication of a humongous $2^{N}$ sized matrix.
If we are able to encode our algorithm in that matrix multiplication, considering the probabilistic interpretation of the output, then we stand a chance of getting that speedup.

As we could see, this model is was simple to understand, being only marginally more complex than that of a classical computer, see also: quantumcomputing.stackexchange.com/questions/6639/is-my-background-sufficient-to-start-quantum-computing/14317#14317 The situation of quantum computers today in the 2020's is somewhat analogous to that of the early days of classical circuits and computers in the 1950's and 1960's, before CPU came along and software ate the world. Even though the exact physics of a classical computer might be hard to understand and vary across different types of integrated circuits, those early hardware pioneers (and to this day modern CPU designers), can usefully view circuits from a higher level point of view, thinking only about concepts such as:

logic gates like AND, NOR and NOT
a clock + registers

as modelled at the register transfer level, and only in a separate compilation step translated into actual chips. This high level understanding of how a classical computer works is what we can call "the programmer's model of a classical computer". So we are now going to describe the quantum analogue of it.

Bibliography:

arxiv.org/pdf/1804.03719.pdf Quantum Algorithm Implementations for Beginners by Abhijith et al. 2020

Timeline of quantum computing

Quantum algorithm

Words: 401 Articles: 16

This is the true key question: what are the most important algorithms that would be accelerated by quantum computing?

Some candidates:

Shor's algorithm: this one will actually make humanity worse off, as we will be forced into post-quantum cryptography that will likely be less efficient than existing classical cryptography to implement
quantum algorithm for linear systems of equations, and related application of systems of linear equations
Grover's algorithm: speedup not exponential. Still useful for anything?
Quantum Fourier transform: TODO is the speedup exponential or not?
Deutsch: solves an useless problem
NISQ algorithms

Do you have proper optimization or quantum chemistry algorithms that will make trillions?

Maybe there is some room for doubt because some applications might be way better in some implementations, but we should at least have a good general idea.

However, clear information on this really hard to come by, not sure why.

Whenever asked e.g. at: physics.stackexchange.com/questions/3390/can-anybody-provide-a-simple-example-of-a-quantum-computer-algorithm/3407 on Physics Stack Exchange people say the infinite mantra:

Lists:

Quantum Algorithm Zoo: the leading list as of 2020
quantum computing computational chemistry algorithms is the area that Ciro and many people are te most excited about is
cstheory.stackexchange.com/questions/3888/np-intermediate-problems-with-efficient-quantum-solutions
mathoverflow.net/questions/33597/are-there-any-known-quantum-algorithms-that-clearly-fall-outside-a-few-narrow-cla

 Tagged

NISQ algorithm

Quantum computers are not expected to solve NP-complete problems

Words: 7

Only NP-intermediate, which includes notably integer factorization:

Quantum Algorithm Zoo

Words: 18

quantumalgorithmzoo.org/

Source on GitHub: github.com/stephenjordan/stephenjordan.github.io

The most comprehensive list is the amazing curated and commented list of quantum algorithms as of 2020.

Quantum algorithm vs quantum gate vs quantum circuit

Words: 65

There is no fundamental difference between them, a quantum algorithm is a quantum circuit, which can be seen as a super complicated quantum gate.

Perhaps the greats practical difference is that algorithms tend to be defined for an arbitrary number of N qubits, i.e. as a function for that each N produces a specific quantum circuit with N qubits solving the problem. Most named gates on the other hand have fixed small sizes.

Quantum algorithm by problem

Articles: 3

Quantum matrix multiplication

cstheory.stackexchange.com/questions/2951/quantum-matrix-multiplication

Quantum algorithm for linear systems of equations

Articles: 1

HHL algorithm

List of quantum algorithms

Words: 153 Articles: 8

Bernstein-Vazirani algorithm

Words: 3

Toy/test/tought experiment algorithm.

Grover's algorithm

Hidden shift algorithm

Articles: 1

Hidden shift problem

Quantum Fourier transform (QFT)

Words: 3

Sample implementations:

Qiskit: qiskit/qft.py

 Tagged

qiskit/qft.py

Shor's algorithm (1994)

Words: 147 Articles: 2

Video 1.

Shor's algorithm Explained by minutephysics (2019)

Source.

How many logical qubits are needed to run Shor's algorithm?

quantumcomputing.stackexchange.com/questions/5048/how-many-logical-qubits-are-needed-to-run-shors-algorithm-efficiently-on-large

Integer factorization algorithms better than Shor's algorithm

Words: 144

2023 www.schneier.com/blog/archives/2023/01/breaking-rsa-with-a-quantum-computer.html comments on "Factoring integers with sublinear resources on a superconducting quantum processor” arxiv.org/pdf/2212.12372.pdf

A group of Chinese researchers have just published a paper claiming that they can—although they have not yet done so—break 2048-bit RSA. This is something to take seriously. It might not be correct, but it’s not obviously wrong.
We have long known from Shor’s algorithm that factoring with a quantum computer is easy. But it takes a big quantum computer, on the orders of millions of qbits, to factor anything resembling the key sizes we use today. What the researchers have done is combine classical lattice reduction factoring techniques with a quantum approximate optimization algorithm. This means that they only need a quantum computer with 372 qbits, which is well within what’s possible today. (The IBM Osprey is a 433-qbit quantum computer, for example. Others are on their way as well.)

Quantum compilation

Words: 312 Articles: 14

Software that maps higher level languages like Qiskit into actual quantum circuits.

Quantum compiler benchmark

Words: 19

These appear to be benchmarks that don't involve running anything concretely, just compiling and likely then counting gates:

github.com/ArlineQ/arline_benchmarks

Quantum Intermediate Representation (QIR)

Words: 29

devblogs.microsoft.com/qsharp/introducing-quantum-intermediate-representation-qir/

Used e.g. by Oxford Quantum Circuits, www.linkedin.com/in/john-dumbell-627454121/ mentions:

Using LLVM to consume QIR and run optimization, scheduling and then outputting hardware-specific instructions.

Presumably the point of it is to allow simulation in classical computers?

Quantum error correction (QEC)

Words: 195 Articles: 9

Technique that uses multiple non-ideal qubits (physical qubits) to simulate/produce one perfect qubit (logical).

One is philosophically reminded of classical error correction codes, where we also have multiple input bits per actual information bit.

TODO understand in detail. This appears to be a fundamental technique since all physical systems we can manufacture are imperfect.

Part of the fundamental interest of this technique is due to the quantum threshold theorem.

For example, when PsiQuantum raised 215M in 2020, they announced that they intended to reach 1 million physical qubits, which would achieve between 100 and 300 logical qubits.

Video 42. "Jeremy O'Brien: "Quantum Technologies" by GoogleTechTalks (2014)" youtu.be/7wCBkAQYBZA?t=2778 describes an error correction approach for a photonic quantum computer.

Bibliography:

errorcorrectionzoo.org/domain/quantum_domain

Quantum error correction code

Articles: 1

Surface code

Quantum threshold theorem

Words: 92 Articles: 6

This theorem roughly states that states that for every quantum algorithm, once we reach a certain level of physical error rate small enough (where small enough is algorithm dependant), then we can perfectly error correct.

This algorithm provides the conceptual division between noisy intermediate-scale quantum era and post-NISQ.

Noisy intermediate-scale quantum era (NISQ)

Words: 49 Articles: 5

Era of quantum computing before we reach physical errors small enough to do perfect quantum error correction as demonstrated by the quantum threshold theorem.

NISQ algorithm

Words: 32 Articles: 4

A quantum algorithm that is thought to be more likely to be useful in the NISQ era of quantum computing.

Variational quantum eigensolver (VQE)

Words: 8

TODO clear example of the computational problem that it solves.

Quantum optimization algorithm

Words: 8 Articles: 2

Quantum approximate optimization algorithm (QAOA)

Words: 8

TODO clear example of the computational problem that it solves.

Quadratic unconstrained binary optimization (QUBO)

High level quantum synthesis

Words: 58 Articles: 1

This is a term "invented" by Ciro Santilli to refer to quantum compilers that are able to convert non-specifically-quantum (functional, since there is no state in quantum software) programs into quantum circuit.

The term is made by adding "quantum" to the more "classical" concept of "high-level synthesis", which refers to software that converts an imperative program into register transfer level hardware, typicially for FPGA applications.

Classiq

www.classiq.io

Quantum computing player

Words: 254 Articles: 12

It is hard to beat the list present at Quantum computing report: quantumcomputingreport.com/players/.

The much less-complete Wikipedia page is also of interest: en.wikipedia.org/wiki/List_of_companies_involved_in_quantum_computing_or_communication It has the merit of having a few extra columns compared to Quantum computing report.

Also of interest: quantumzeitgeist.com/interactive-map-of-quantum-computing-companies-from-around-the-globe/

Quantum computing player in Brazil

Words: 162

Paulo Nussenzveig physics researcher at University of São Paulo. Laboratory page: portal.if.usp.br/lmcal/pt-br/node/323: LMCAL, laboratory of coherent manipulation of atoms and light. Google Scholar: scholar.google.com/citations?user=FbGL0BEAAAAJ
Brazil Quantum: interest group created by students. Might be a software consultancy: www.terra.com.br/noticias/tecnologia/inovacao/pesquisadores-paulistas-tentam-colocar-brasil-no-mapa-da-computacao-quantica,2efe660fbae16bc8901b1d00d139c8d2sz31cgc9.html
DOBSLIT dobslit.com/en/the-company/ company in São Carlos, as of 2022 a quantum software consultancy with 3 people: www.linkedin.com/search/results/people/?currentCompany=%5B%2272433615%22%5D&origin=COMPANY_PAGE_CANNED_SEARCH&sid=TAj two of them from the Federal University of São Carlos
computacaoquanticabrasil.com/ Website half broken as of 2022. Mentions a certain Lagrange Foundation, but their website is down.
QuInTec academic interest group
- www.terra.com.br/noticias/tecnologia/inovacao/pesquisadores-paulistas-tentam-colocar-brasil-no-mapa-da-computacao-quantica,2efe660fbae16bc8901b1d00d139c8d2sz31cgc9.html mentions 6 professors, 3 from USP 3 from UNICAMP interest group:
- drive.google.com/file/d/1geGaRuCpRHeuLH2MLnLoxEJ1iOz4gNa9/view white paper gives all names
  - Celso Villas-Bôas
  - Frederico Brito
  - Gustavo Wiederhecker
  - Marcelo Terra Cunha
  - Paulo Nussenzveig
  - Philippe Courteille
- sites.google.com/unicamp.br/quintec/home their website.
- a 2021 symposium they organized: www.saocarlos.usp.br/dia-09-quintec-quantum-engineering-workshop/ some people of interest:
  - Samuraí Brito www.linkedin.com/in/samuraí-brito-4a57a847/ at Itaú Unibanco, a Brazilian bank
  - www.linkedin.com/in/dario-sassi-thober-5ba2923/ from wvblabs.com.br/
  - www.linkedin.com/in/roberto-panepucci-phd from en.wikipedia.org/wiki/Centro_de_Pesquisas_Renato_Archer in Campinas
Quanby quantum software in Florianópolis, founder Eduardo Duzzioni
thequantumhubs.com/category/quantum-brazil-news/ good links
qubit.lncc.br/?lang=en Quantum Computing Group of the National Laboratory for Scientific Computing: pt.wikipedia.org/wiki/Laboratório_Nacional_de_Computação_Científica in Rio. The principal researcher seems to be www.lncc.br/~portugal/. He knows what GitHub is: github.com/programaquantica/tutoriais, PDF without .tex though.
quantum-latino.com/ conference. E.g. 2022: www.canva.com/design/DAFErjU3Wvk/2xo25nEuqv9O7RbCPLNEkw/view

Quantum computing company

 Tagged

Sandbox AQ

Quantum computing research institute

Words: 10 Articles: 2

QuTech

Words: 10 Articles: 1

QuTech Academy

Words: 10

One of their learning sites: www.qutube.nl/

The educational/outreach branch of QuTech.

qutechacademy.nl/

www.youtube.com/@QuTechAcademy

Organization developing quantum hardware

Words: 8 Articles: 2

 Tagged

Organization developing carbon nanotube spin quantum computer
Organization developing neutral atom quantum computer
Organization developing photonic quantum computer
Organization developing superconducting quantum computer
Organization developing trapped ion quantum computer

D-Wave Systems

Words: 1

Vaporware?

ColdQuanta (2007)

Words: 7

Not a quantum computing pure-play, they also do sensing.

Organization developing quantum software

Words: 38 Articles: 3

 Tagged

Cambridge Quantum Computing
Classiq
List of quantum control systems
Organization developing quantum control systems

Quantum Computing Inc.

Words: 19

Really weird and obscure company, good coverage: thequantuminsider.com/2020/02/06/quantum-computing-incorporated-the-first-publicly-traded-quantum-computing-stock/

Publicly traded in 2007, but only pivoted to quantum computing much later.

Social media:

Microsoft Quantum

Phasecraft (2018)

Words: 19

www.phasecraft.io

The co-founder's name, Toby Cubitt, is the mos awesome thing ever (Cubitt -> qubit). From UCL.

Funding:

2023: £13m: www.uktech.news/deep-tech/phasecraft-quantum-computing-20230816

Quantum computing paradigm

Quantum computing hardware

Words: 7k Articles: 127

Step of operation of a quantum computer

Articles: 2

State initialization (quantum computing)

Readout (quantum computing)

Quantum computers as experiments that are hard to predict outcomes

Words: 189

One possibly interesting and possibly obvious point of view, is that a quantum computer is an experimental device that executes a quantum probabilistic experiment for which the probabilities cannot be calculated theoretically efficiently by a nuclear weapon.

This is how quantum computing was originally theorized by the likes of Richard Feynman: they noticed that "Hey, here's a well formulated quantum mechanics problem, which I know the algorithm to solve (calculate the probability of outcomes), but it would take exponential time on the problem size".

The converse is then of course that if you were able to encode useful problems in such an experiment, then you have a computer that allows for exponential speedups.

This can be seen very directly by studying one specific quantum computer implementation. E.g. if you take the simplest to understand one, photonic quantum computer, you can make systems for which you need exponential time to calculate the probabilities that photons will exit through certain holes and not others.

The obvious aspect of this idea is by coming from quantum logic gates are needed because you can't compute the matrix explicitly as it grows exponentially: knowing the full explicit matrix is impossible in practice, and knowing the matrix is equivalent to knowing the probabilities of every outcome.

Quantum computing is hard because we want long coherence but fast control

Words: 29

Mentioned e.g. at:

These are two conflicting constraints:

long coherence times: require isolation from external world, otherwise observation destroys quantum state
fast control and readout: require coupling with external world

Quantum computer type

Words: 2k Articles: 33

Model of quantum computing

Words: 2k Articles: 32

Measurement and circuit based quantum computers

Words: 48 Articles: 2

Circuit-based quantum computer

Words: 4

Synonym to gate-based quantum computer/digital quantum computer?

Measurement-based quantum computer (One-way quantum computer)

Words: 44

TODO confirm: apparently in the paradigm you can choose to measure only certain output qubits.

This makes things irreversible (TODO what does reversibility mean in this random context?), as opposed to Circuit-based quantum computer where you measure all output qubits at once.

TODO what is the advantage?

Analog and digital quantum computers

Words: 2k Articles: 28

Digital quantum computer (Gate-based quantum computer)

Words: 2k Articles: 25

As of 2022, this tends to be the more "default" when you talk about a quantum computer.

But there are some serious analog quantum computer contestants in the field as well.

Quantum circuit

Words: 449 Articles: 3

A quantum circuit is a graph of quantum logic gates.

Quantum circuits are the prevailing model of quantum computing as of the 2010's - 2020's

 Tagged

Bell circuit

Quantum state vector

Tensor product in quantum computing

Words: 196

We don't need to understand a super generalized version of tensor products to know what they mean in basic quantum computing!

Intuitively, taking a tensor product of two qubits simply means putting them together on the same quantum system/computer.

When we write the bra-ket notation:

∣ 00 ⟩

that is the same as

∣ 0 ⟩ \otimes ∣ 0 ⟩

The tensor product is called a "product" because it distributes over addition.

E.g. consider:

(\frac{∣ 0 ⟩ + ∣ 1 ⟩}{2}) \otimes ∣ 0 ⟩ = \frac{∣ 0 ⟩ \otimes ∣ 0 ⟩ + ∣ 1 ⟩ \otimes ∣ 0 ⟩}{2} = \frac{∣ 00 ⟩ + ∣ 10 ⟩}{2}

(6)

Intuitively, in this operation we just put a Hadamard gate qubit together with a second pure

∣ 0 ⟩

qubit.

And the outcome still has the second qubit as always 0, because we haven't made them interact.

The quantum state

\frac{∣ 00 ⟩ + ∣ 10 ⟩}{2}

is called a separable state, because it can be written as a single product of two different qubits. We have simply brought two qubits together, without making them interact.

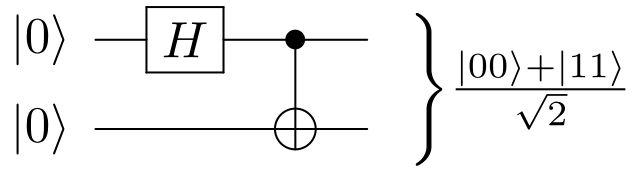
If we then add a CNOT gate to make a Bell state:

\frac{∣ 00 ⟩ + ∣ 11 ⟩}{2} = \frac{∣ 0 ⟩ \otimes ∣ 0 ⟩ + ∣ 1 ⟩ \otimes ∣ 1 ⟩}{2}

(7)

we can now see that the Bell state is non-separable: we've made the two qubits interact, and there is no way to write this state with a single tensor product. The qubits are fundamentally entangled.

Quantum circuits vs classical circuits

Words: 239

Just like a classic programmer does not need to understand the intricacies of how transistors are implemented and CMOS semiconductors, the quantum programmer does not understand physical intricacies of the underlying physical implementation.

The main difference to keep in mind is that quantum computers cannot save and observe intermediate quantum state, so programming a quantum computer is basically like programming a combinatorial-like circuit with gates that operate on (qu)bits:

For this reason programming a quantum computer is much like programming a classical combinatorial circuit as you would do with SPICE, verilog-or-vhdl, in which you are basically describing a graph of gates that goes from the input to the output

For this reason, we can use the words "program" and "circuit" interchangeably to refer to a quantum program

Also remember that and there is no no clocks in combinatorial circuits because there are no registers to drive; and so there is no analogue of clock in the quantum system either,

Another consequence of this is that programming quantum computers does not look like programming the more "common" procedural programming languages such as C or Python, since those fundamentally rely on processor register / memory state all the time.

Quantum programmers can however use classic languages to help describe their quantum programs more easily, for example this is what happens in Qiskit, where you write a Python program that makes Qiskit library calls that describe the quantum program.

Quantum logic gate

Words: 2k Articles: 20

At Section "Quantum computing is just matrix multiplication" we saw that making a quantum circuit actually comes down to designing one big unitary matrix.

We have to say though that that was a bit of a lie.

Quantum programmers normally don't just produce those big matrices manually from scratch.

Instead, they use quantum logic gates.

The following are the main reasons for that:

Section "Quantum logic gates are needed because you can't compute the matrix explicitly as it grows exponentially"
Section "Quantum logic gates are needed for physical implementation"

Quantum logic gates are needed because you can't compute the matrix explicitly as it grows exponentially

Words: 386

One key insight, is that the matrix of a non-trivial quantum circuit is going to be huge, and won't fit into any amount classical memory that can be present in this universe.

This is because the matrix is exponential in the number qubits, and

2^{100}

is more than the number of atoms in the universe!

Therefore, off the bat we know that we cannot possibly describe those matrices in an explicit form, but rather must use some kind of shorthand.

But it gets worse.

Even if we had enough memory, the act of explicitly computing the matrix is not generally possible.

This is because knowing the matrix, basically means knowing the probability result for all possible

2^{N}

outputs for each of the

2^{N}

possible inputs.

But if we had those probabilities, our algorithmic problem would already be solved in the first place! We would "just" go over each of those output probabilities (OK, there are

2^{N}

of those, which is also an insurmountable problem in itself), and the largest probability would be the answer.

So if we could calculate those probabilities on a classical machine, we would also be able to simulate the quantum computer on the classical machine, and quantum computing would not be able to give exponential speedups, which we know it does.

To see this, consider that for a given input, say 000 on a 3 qubit machine, the corresponding 8-sized quantum state looks like:

000 -> 1000 0000 == (1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)

and therefore when you multiply it by the unitary matrix of the quantum circuit, what you get is the first column of the unitary matrix of the quantum circuit. And 001, gives the second column and so on.

As a result, to prove that a quantum algorithm is correct, we need to be a bit smarter than "just calculate the full matrix".

Which is why you should now go and read: Section "Quantum algorithm".

This type of thinking links back to how physical experiments relate to quantum computing: a quantum computer realizes a physical experiment to which we cannot calculate the probabilities of outcomes without exponential time.

So for example in the case of a photonic quantum computer, you are not able to calculate from theory the probability that photons will show up on certain wires or not.

Quantum logic gates are needed for physical implementation

Words: 376

One direct practical reason is that we need to map the matrix to real quantum hardware somehow, and all quantum hardware designs so far and likely in the future are gate-based: you manipulate a small number of qubits at a time (2) and add more and more of such operations.

While there are "quantum compilers" to increase the portability of quantum programs, it is to be expected that programs manually crafted for a specific hardware will be more efficient just like in classic computers.

TODO: is there any clear reason why computers can't beat humans in approximating any unitary matrix with a gate set?

This is analogous to what classic circuit programmers will do, by using smaller logic gates to create complex circuits, rather than directly creating one huge truth table.

The most commonly considered quantum gates take 1, 2, or 3 qubits as input.

The gates themselves are just unitary matrices that operate on the input qubits and produce the same number of output qubits.

For example, the matrix for the CNOT gate, which takes 2 qubits as input is:

The final question is then: if I have a 2 qubit gate but an input with more qubits, say 3 qubits, then what does the 2 qubit gate (4x4 matrix) do for the final big 3 qubit matrix (8x8)? In order words, how do we scale quantum gates up to match the total number of qubits?

The intuitive answer is simple: we "just" extend the small matrix with a larger identity matrix so that the sum of the probabilities third bit is unaffected.

More precisely, we likely have to extend the matrix in a way such that the partial measurement of the original small gate qubits leaves all other qubits unaffected.

For example, if the circuit were made up of a CNOT gate operating on the first and second qubits as in:

0 ----+----- 0
      |
1 ---CNOT--- 1

2 ---------- 2

then we would just extend the 2x2 CNOT gate to:

TODO lazy to properly learn right now. Apparently you have to use the Kronecker product by the identity matrix. Also, zX-calculus appears to provide a powerful alternative method in some/all cases.

Bibliography:

quantumcomputing.stackexchange.com/questions/2299/how-to-interpret-a-quantum-circuit-as-a-matrix

Universal quantum gates

Words: 117

Just like as for classic gates, we would like to be able to select quantum computer physical implementations that can represent one or a few gates that can be used to create any quantum circuit.

Unfortunately, in the case of quantum circuits this is obviously impossible, since the space of N x N unitary matrices is infinite and continuous.

Therefore, when we say that certain gates form a "set of universal quantum gates", we actually mean that "any unitary matrix can be approximated to arbitrary precision with enough of these gates".

Or if you like fancy Mathy words, you can say that the subgroup of the unitary group generated by our basic gate set is a dense subset of the unitary group.

 Tagged

Clifford plus T

Single-qubit gate

Words: 620 Articles: 12

The first two that you should study are:

Quantum NOT gate
Hadamard gate
Phase shift gate

Hadamard gate

Words: 39

The Hadamard gate takes

∣ 0 ⟩

∣ 1 ⟩

(quantum states with probability 1.0 of measuring either 0 or 1), and produces states that have equal probability of 0 or 1.

H = \frac{1}{2} [11 1 - 1]

(8)

Equation 8.

Hadamard gate matrix

Figure 1.
Hadamard gate symbol
. Source.

Pauli gate

Words: 73 Articles: 3

Pauli-X gate (Quantum NOT gate)

Words: 73

The quantum NOT gate swaps the state of

∣ 0 ⟩

and

∣ 1 ⟩

, i.e. it maps:

x ∣ 0 ⟩ + y ∣ y ⟩ \to y ∣ 0 ⟩ + x ∣ y ⟩

(9)

As a result, this gate also inverts the probability of measuring 0 or 1, e.g.

if the old probability of 0 was 0, then it becomes 1
if the old probability of 0 was 0.2, then it becomes 0.8

[0110]

(10)

Equation 10.

Quantum NOT gate matrix

Figure 2.
Quantum NOT gate symbol
. Source.

Pauli-Y gate

Pauli-Z gate

 Tagged

CZ gate

Phase shift gate

Multi-qubit gate

Words: 500 Articles: 5

The most common way to construct multi-qubit gates is to use single-qubit gates as part of a controlled quantum gate.

Controlled quantum gate

Words: 486 Articles: 3

Controlled quantum gates are gates that have two types of input qubits:

control qubits
operand qubits (terminology made up by Ciro Santilli just now)

These gates can be understood as doing a certain unitary operation only if the control qubits are enabled or disabled.

The first example to look at is the CNOT gate.

Figure 3.
Generic controlled quantum gate symbol
. Source.
The black dot means "control qubit", and "U" means an arbitrary Unitary operation.
When the operand has a conventional symbol, e.g. the Figure 2. "Quantum NOT gate symbol" for the quantum NOT gate to form the CNOT gate, that symbol is used in the operand instead.

Empty circle control qubit notation

Words: 27

Some authors use the convention of:

filled black circle: conventional controlled quantum gate, i.e. operate if control qubit is active
empty (White) circle: operate if control qubit is inactive

CNOT gate (Controlled NOT gate)

Words: 378

The CNOT gate is a controlled quantum gate that operates on two qubits, flipping the second (operand) qubit if the first (control) qubit is set.

This gate is the first example of a controlled quantum gate that you should study.

1000010000010010

(11)

Equation 11.

CNOT gate matrix

Figure 4.
CNOT gate symbol
. Source. The symbol follow the generic symbol convention for controlled quantum gates shown at Figure 3. "Generic controlled quantum gate symbol", but replacing the generic "U" with the Figure 2. "Quantum NOT gate symbol".

To understand why the gate is called a CNOT gate, you should think as follows.

First let's produce a generic quantum state vector where the control qubit is certain to be 0.

On the standard basis:

∣ 00 ⟩ ∣ 01 ⟩ ∣ 10 ⟩ ∣ 11 ⟩

(12)

we see that this means that only

∣ 00 ⟩

and

∣ 01 ⟩

should be possible. Therefore, the state must be of the form:

x y 00

(13)

where

x

and

y

are two complex numbers such that

∣ x ∣ + ∣ y ∣ = 1.0

If we operate the CNOT gate on that state, we obtain:

1000010000010010 \times x y 00 = x y 00

(14)

and so the input is unchanged as desired, because the control qubit is 0.

If however we take only states where the control qubit is for sure 1:

1000010000010010 \times 00 x y = 00 y x

(15)

Therefore, in that case, what happened is that the probabilities of

∣ 10 ⟩

and

∣ 11 ⟩

were swapped from

x

and

y

y

and

x

respectively, which is exactly what the quantum NOT gate does.

So from this we understand more concretely what "the gate only operates if the first qubit is set to one" means.

Now go and study the Bell state and understand intuitively how this gate is used to produce it.

CZ gate

Toffoli gate

Clifford gates

Words: 89 Articles: 2

This gate set alone is not a set of universal quantum gates.

Notably, circuits containing those gates alone can be fully simulated by classical computers according to the Gottesman-Knill theorem, so there's no way they could be universal.

This means that if we add any number of Clifford gates to a quantum circuit, we haven't really increased the complexity of the algorithm, which can be useful as a transformational device.

A popular set of universal quantum gates derived from Clifford gates is Clifford plus T.

Clifford plus T

Words: 14

Set of quantum logic gate composed of the Clifford gates plus the Toffoli gate. It forms a set of universal quantum gates.

Gottesman-Knill theorem

List of quantum logic gates

Analog quantum computer

Words: 169 Articles: 1

quantumtech.blog/2023/01/17/quantum-computing-with-neutral-atoms/ OK this one hits it:
As Alex Keesling, CEO of QuEra told me, "... whereas in gate-based [digital] quantum computing the focus is on the sequence of the gates, in analog quantum processing it's more about the position of the atoms and where you place them so they can mirror real life problems. We arrange the atoms and define the forces that drive them and then measure the result... so it’s a geometric encoding of the problem itself."
So we understand that it is truly like the classical computer analog vs digital case.
thequantuminsider.com/2022/06/28/why-analog-neutral-atoms-quantum-computing-is-a-promising-direction-for-early-quantum-advantage on The Quantum Insider useless article mostly by Pasqal

Video 2.

TensorFlow quantum by Masoud Mohseni (2020)

Source. At the timestamp, Masoud gives a thought experiment example of the perhaps simplest to understand analog quantum computer: chained double-slit experiments with carefully calculated distances between slits. Calulating the final propability distribution of that grows exponentially.

 Tagged

Pasqal
QuEra

Continuous-variable quantum information

Words: 40

TODO synonym to analog quantum computer?

It is also possible to carry out quantum computing without qubits using processes with a continuous spectrum of measurement.

As of 2020, these approaches seem less developed/promising, but who knows.

These computers can be seen as analogous to classical non-quantum analog computers.

Quantum computer physical implementation

Words: 4k Articles: 84

Lists of the most promising implementations:

As of 2020, the hottest by far are:

superconducting quantum computer
trapped ion quantum computer
photonic quantum computer

Video 3.

How To Build A Quantum Computer by Lukas's Lab (2023)

Source.

Super quick overview of the main types of quantum computer physical implementations, so doesn't any much to a quick Google.

He says he's going to make a series about it, so then something useful might actually come out. The first one was: Video 11. "How to Turn Superconductors Into A Quantum Computer by Lukas's Lab (2023)", but it is still too basic.

The author's full name is Lukas Baker, www.linkedin.com/in/lukasbaker1331/, found with Google reverse image search, even though the LinkedIn image is very slightly different from the YouTube one.

As of 2023 he was a PhD student at NYU.

Carbon nanotube spin quantum computer

Words: 67 Articles: 3

www.ucl.ac.uk/quantum-devices/carbon-nanotube-spin-qubits

Organization developing carbon nanotube spin quantum computer

Words: 67 Articles: 2

C12 Quantum Electronics

Words: 67 Articles: 1

Official website: www.c12qe.com/

2024 address: 26 rue des Fossés Saint-Jacques, 75005 Paris

www.c12qe.com/articles/la-deeptech-c12-inaugure-sa-premiere-ligne-de-production-de-puces-quantiques-a-paris explains their choice of address: there is a hill in the 5th arrondissement of Paris, and they have a lab in a deep basement, which helps reduce vibrations from the external environment. Interesting.

Crunchbase entry: www.crunchbase.com/organization/c12-quantum-electronics

Founed by two twin brothers who both studied at École Polytechnique: Pierre Desjardins and Matthieu Desjardins.

Funding:

UCL Quantum Devices Group

Words: 9

www.ucl.ac.uk/quantum-devices/carbon-nanotube-spin-qubits As mentioned in this link, they collaborate with C12 Quantum Electronics.

Diamond vacancy quantum computer

Words: 2 Articles: 2

thequantuminsider.com/2022/03/31/5-quantum-computing-companies-working-with-nv-centre-in-diamond-technology/ on The Quantum Insider

Principal investigator: Mark Buitelaar

N-V center quantum computer

Nitrogen-vacancy center

Electron on helium quantum computer (eHe quantum computer)

Articles: 2

Organization developing electron on helium quantum computer

Articles: 1

EeroQ

eeroq.com/

Nuclear magnetic resonance quantum computer

Words: 59 Articles: 4

Organization developing nuclear magnetic resonance quantum computer

Words: 59 Articles: 3

 Tagged

Atom Computing

Silicon Quantum Computing (2017-)

Words: 59 Articles: 2

sqc.com.au/2024/02/08/silicon-quantum-computing-demonstrates-high-fidelity-initialisation-of-nuclear-spins-in-a-4-qubit-device/ points to one of their papers: www.nature.com/articles/s41565-023-01596-9 High-fidelity initialization and control of electron and nuclear spins in a four-qubit register

Their approach seems to be more precisely called: Kane quantum computer and uses phosphorus embedded in silicon.

They come from the University of New South Wales.

Kane quantum computer

Words: 12

Through the company Silicon Quantum Computing, this has been Australia's national quantum computing focus.

Diraq

Words: 11

Another Australian company and using a similar approach as Silicon Quantum Computing:

Some coverage at: www.afr.com/technology/start-up-says-it-will-have-a-quantum-computer-by-2028-20240219-p5f64k

Quantum dot quantum computer

Words: 14 Articles: 3

Organization developing quantum dot quantum computer

Words: 5 Articles: 1

Quantum Motion (2017)

Words: 5

Funding:

2023: £42m (~$50m) www.uktech.news/deep-tech/quantum-motion-raises-42m-20230221

Intel quantum computer

Words: 9

Video 4.

Architecture All Access: Quantum Computing by James Clarke (2021)

Source.

Superconducting quantum computing

Words: 2k Articles: 33

Based on the Josephson effect. Yet another application of that phenomenal phenomena!

Philosophically, superconducting qubits are good because superconductivity is macroscopic.

It is fun to see that the representation of information in the QC basically uses an LC circuit, which is a very classical resonator circuit.

As mentioned at en.wikipedia.org/wiki/Superconducting_quantum_computing#Qubit_archetypes there are actually a few different types of superconducting qubits:

flux
charge
phase

and hybridizations of those such as:

transmon

Input:

microwave radiation to excite circuit, or do nothing and wait for it to fall to 0 spontaneously
interaction: TODO
readout: TODO

Video 5.

Quantum Computing with Superconducting Qubits by Alexandre Blais (2012)

Source.

youtu.be/t5nxusm_Umk?t=176 quantum computing is hard because we want long coherence but fast control
youtu.be/t5nxusm_Umk?t=784 superconducting quantum computer need non-linear components

Video 6.

Quantum Transport, Lecture 16: Superconducting qubits by Sergey Frolov (2013)

Source. youtu.be/Kz6mhh1A_mU?t=1171 describes several possible realizations: charge, flux, charge/flux and phase.

Video 7.

Building a quantum computer with superconducting qubits by Daniel Sank (2019)

Source. Daniel wears a "Google SB" t-shirt, which either means shabi in Chinese, or Santa Barbara. Google Quantum AI is based in Santa Barbara, with links to UCSB.

youtu.be/uPw9nkJAwDY?t=293 superconducting qubits are good because superconductivity is macroscopic. Explains how in non superconducting metal, each electron moves separatelly, and can hit atoms and leak vibration/photos, which lead to observation and quantum error
youtu.be/uPw9nkJAwDY?t=429 made of aluminium
youtu.be/uPw9nkJAwDY?t=432 shows the circuit diagram, and notes that the thing is basically a LC circuit
```
+-----+
|     |
|   +-+-+
|   |   |
C   X   X
|   |   |
|   +-+-+
|     |
+-----+
```
using the newly created just now Ciro's ASCII art circuit diagram notation. Note that the block on the right is a SQUID device.
youtu.be/uPw9nkJAwDY?t=471 mentions that the frequency between states 0 and 1 is chosen to be 6 GHz:
- higher frequencies would be harder/more expensive to generate
- lower frequencies would mean less energy according to the Planck relation. And less energy means that thermal energy would matter more, and introduce more noise.
  6 GHz is about $6^{9} \times h = 6 \times 1 0^{9} \times 6.62 \times 1 0^{- 34} \approx 4 \times 1 0^{- 24} J$
  From the definition of the Boltzmann constant, the temperature which has that average energe of particles is of the order of:
  $T = E / k_{b} = 4 \times 1 0^{- 24} /1.38 \times 1 0^{- 23} \approx 0.3 K$
  (16)
This explains why we need to go to much lower temperatures than simply the superconducting temperature of aluminum!

Video 8.

A Brief History of Superconducting quantum computing by Steven Girvin (2021)

Source.

youtu.be/xjlGL4Mvq7A?t=138 superconducting quantum computer need non-linear components (too brief if you don't know what he means in advance)
youtu.be/xjlGL4Mvq7A?t=169 quantum computing is hard because we want long coherence but fast control

Video 9.

Superconducting Qubits I Part 1 by Zlatko Minev (2020)

Source.

The Q&A in the middle of talking is a bit annoying.

youtu.be/eZJjQGu85Ps?t=2443 the first actually useful part, shows a transmon diagram with some useful formulas on it

Video 10.

Superconducting Qubits I Part 2 by Zlatko Minev (2020)

Source.

Video 11.

How to Turn Superconductors Into A Quantum Computer by Lukas's Lab (2023)

Source. This video is just the introduction, too basic. But if he goes through with the followups he promisses, then something might actually come out of it.

Superconducting quantum computer need non-linear components

Words: 66

Non-linearity is needed otherwise the input energy would just make the state go to higher and higher energy levels, e.g. from 1 to 2. But we only want to use levels 0 and 1.

The way this is modelled in by starting from a pure LC circuit, which is an harmonic oscillator, see also quantum LC circuit, and then replacing the linear inductor with a SQUID device, e.g. mentioned at: youtu.be/eZJjQGu85Ps?t=1655 Video 9. "Superconducting Qubits I Part 1 by Zlatko Minev (2020)".

Superconducting qubit

Words: 691 Articles: 12

Pros and cons of superconducting qubits

Words: 225 Articles: 5

Con of superconducting qubits

Words: 82 Articles: 1

requires intense refrigeration to 15mK in dilution refrigerator. Note that this is much lower than the actual superconducting temperature of the metal, we have to go even lower to reduce noise enough, see e.g. youtu.be/uPw9nkJAwDY?t=471 from Video 7. "Building a quantum computer with superconducting qubits by Daniel Sank (2019)"
less connectivity, normally limited to 4 nearest neighbours, or maybe 6 for 3D approaches, e.g. compared to trapped ion quantum computers, where each trapped ion can be entangled with every other on the same chip

Superconducting qubits are bad because it is harder to ensure that they are all the same

Words: 18

This is unlike atomic systems like trapped ion quantum computers, where each atom is necessarily exactly the same as the other.

Pro of superconducting qubits

Words: 143 Articles: 2

Superconducting qubits are good because superconductivity is macroscopic

Words: 106

Superconducting qubits are regarded as promising because superconductivity is a macroscopic quantum phenomena of Bose Einstein condensation, and so as a macroscopic phenomena, it is easier to control and observe.

This is mentioned e.g. in this relatively early: physicsworld.com/a/superconducting-quantum-bits/. While most quantum phenomena is observed at the atomic scale, superconducting qubits are micrometer scale, which is huge!

Physicists are comfortable with the use of quantum mechanics to describe atomic and subatomic particles. However, in recent years we have discovered that micron-sized objects that have been produced using standard semiconductor-fabrication techniques – objects that are small on everyday scales but large compared with atoms – can also behave as quantum particles.

Superconducting qubits are bad because of fabrication variation

Words: 37

Atom-based qubits like trapped ion quantum computers have parameters fixed by the laws of physics.

However superconducting qubits have a limit on how precise their parameters can be set based on how well we can fabricate devices. This may require per-device characterisation.

Superconducting qubit type

Words: 466 Articles: 5

Flux qubit

Words: 211

In Ciro's ASCII art circuit diagram notation, it is a loop with three Josephson junctions:

+----X-----+
|          |
|          |
|          |
+--X----X--+

https://upload.wikimedia.org/wikipedia/en/0/04/Flux_Qubit_-_Holloway.jpg

Video 12.

Superconducting Qubit by NTT SCL (2015)

Source.

Offers an interesting interpretation of superposition in that type of device (TODO precise name, seems to be a flux qubit): current going clockwise or current going counter clockwise at the same time. youtu.be/xjlGL4Mvq7A?t=1348 clarifies that this is just one of the types of qubits, and that it was developed by Hans Mooij et. al., with a proposal in 1999 and experiments in 2000. The other type is dual to this one, and the superposition of the other type is between N and N + 1 copper pairs stored in a box.

Their circuit is a loop with three Josephson junctions, in Ciro's ASCII art circuit diagram notation:

+----X-----+
|          |
|          |
|          |
+--X----X--+

They name the clockwise and counter clockwise states

∣ L ⟩

and

∣ R ⟩

(named for Left and Right).

When half the magnetic flux quantum is applied as microwaves, this produces the ground state:

∣ 0 ⟩ = ∣ L ⟩ + ∣ R ⟩

(17)

where

L

and

R

cancel each other out. And the first excited state

∣ 1 ⟩

is:

∣ 0 ⟩ = ∣ L ⟩ - ∣ R ⟩

(18)

Then he mentions that:

to go from 0 to 1, they apply the difference in energy
if the duration is reduced by half, it creates a superposition of $∣ 0 ⟩ + ∣ 1 ⟩$ .

Transmon (2007)

Words: 255 Articles: 3

Used e.g. in the Sycamore processor.

The most basic type of transmon is in Ciro's ASCII art circuit diagram notation, an LC circuit e.g. as mentioned at youtu.be/cb_f9KpYipk?t=180 from Video 15. "The transmon qubit by Leo Di Carlo (2018)":

+----------+
| Island 1 |
+----------+
   |   |
   X   C
   |   |
+----------+
| Island 2 |
+----------+

youtu.be/eZJjQGu85Ps?t=2443 from Video 9. "Superconducting Qubits I Part 1 by Zlatko Minev (2020)" describes a (possibly simplified) physical model of it, as two superconducting metal islands linked up by a Josephson junction marked as X in the diagram as per-Ciro's ASCII art circuit diagram notation:

+-------+       +-------+
|       |       |       |
| Q_1() |---X---| Q_2() |
|       |       |       |
+-------+       +-------+

The circuit is then analogous to a LC circuit, with the islands being the capacitor. The Josephson junction functions as a non-linear inductor.

Others define it with a SQUID device instead: youtu.be/cb_f9KpYipk?t=328 from Video 15. "The transmon qubit by Leo Di Carlo (2018)". He mentions that this allows tuning the inductive element without creating a new device.

Video 13.

The superconducting transmon qubit as a microwave resonator by Daniel Sank (2021)

Source.

Video 14.

Calibration of Transmon Superconducting Qubits by Stefan Titus (2021)

Source. Possibly this Keysight which would make sense.

An Introduction to the Transmon Qubit for Electromagnetic Engineers (2021)

Words: 5

arxiv.org/abs/2106.11352

This is a good review article.

Rabi cycle (Rabi oscillations)

The Hardware of a Quantum Computer by TU Delft

Words: 101

EdX course. Meh! Just give me the YouTube list!!

But seriously, this is a valuable little list.

The course is basically exclusively about transmons.

Video 15.

The transmon qubit by Leo Di Carlo (2018)

Source. Via QuTech Academy.

Video 16.

Circuit QED by Leo Di Carlo (2018)

Source. Via QuTech Academy.

Video 17.

Measurements on transmon qubits by Niels Bultink (2018)

Source. Via QuTech Academy. I wish someone would show some actual equipment running! But this is of interest.

Video 18.

Single-qubit gate by Brian Taraskinki (2018)

Source. Good video! Basically you make a phase rotation by controlling the envelope of a pulse.

Video 19.

Two qubit gates by Adriaan Rol (2018)

Source.

Video 20.

Assembling a Quantum Processor by Leo Di Carlo (2018)

Source. Via QuTech Academy.

Organization developing superconducting quantum computer

Words: 573 Articles: 18

Alice&Bob

Words: 58 Articles: 1

Funding rounds:

January 2025: 100M Euros^[ref]
March 2022: 27M Euros

About their qubit:

alice-bob.com/2023/02/15/computing-256-bit-elliptic-curve-logarithm-in-9-hours-with-126133-cat-qubits/ Computing 256-bit elliptic curve logarithm in 9 hours with 126,133 cat qubits (2023). This describes their "cat qubit".

Video 21.

Cat Qubits and LDPC Codes, a New Step Towards Quantum Error Correction by Alice&Bob

. Source.

Video 22.

Behind The Tech : Cryostats by Alice&Bob

. Source. Showcasing their Bluefors dilution refrigerators. They are named after Asterix characters.

Cat qubit

Google Quantum AI

Words: 294 Articles: 8

Google's quantum hardware/software effort.

The "AI" part is just prerequisite buzzword of the AI boom era for any project and completely bullshit.

According to job postings such as: archive.ph/wip/Fdgsv their center is in Goleta, California, near Santa Barbara. Though Google tends to promote it more as Santa Barbara, see e.g. Daniel's t-shirt at Video 7. "Building a quantum computer with superconducting qubits by Daniel Sank (2019)".

Video 23.

Control of transmon qubits using a cryogenic CMOS integrated circuit (QuantumCasts) by Google (2020)

Source. Fantastic video, good photos of the Google Quantum AI setup!

Google Quantum Campus

Words: 32

Built 2021. TODO address. Located in Santa Barbara, which has long been the epycenter of Google's AI efforts. Apparently contains fabrication facilities.

Announcement: blog.google/technology/ai/unveiling-our-new-quantum-ai-campus/

Video 24.

Take a tour of Google's Quantum AI Lab by Google Quantum AI

. Source. 2023

Google Quantum AI employee

Words: 103 Articles: 3

Daniel Sank

Words: 35

Cool dude. Uses Stack Exchange: physics.stackexchange.com/users/31790/danielsank

Started at Google Quantum AI in 2014.

Has his LaTeX notes at: github.com/DanielSank/theory. One day he will convert to OurBigBook.com. Interesting to see that he is able to continue his notes despite being at Google.

Julian Kelly

Words: 47

Timeline:

2015: joined Google as a Google Quantum AI employee
2010: UCSB Physics PhD. His thesis was "Fault-tolerant superconducting qubits" and the PDF can be downloaded from: alexandria.ucsb.edu/lib/ark:/48907/f3b56gwb.
2006: UCSB Physics undergrad. In 2008 he joined John Martinis' lab during his undergrad itself.

He went pretty much in a straight line into the quantum computing boom! Well done.

Figure 7. Source.

John M. Martinis

Words: 21

Timeline:

2020: left Google after he was demoted apparently, and joined Silicon Quantum Computing.
2014: he and the entire lab were hired by Google

Google Quantum AI hardware

Words: 91 Articles: 2

Sycamore processor

Words: 73

This is a good read: quantumai.google/hardware/datasheet/weber.pdf May 14, 2021. Their topology is so weird, not just a rectangle, one wonders why! You get different error rates in different qubits, it's mad.

Figure 9.
Google Sycamore Weber quantum computer connectivity graph
. Weber is a specific processor of the Sycamore family. From this we see it clearly that qubits are connected to at most 4 other qubits, and that the full topology is not just a simple rectangle.

Willow (quantum computer)

Words: 18

Video 25.

Meet Willow, our state-of-the-art quantum chip by Google Quantum AI

. Source.

2024 public presentation of their then new chip.

IBM Quantum Computing (IBM Q)

Words: 36 Articles: 1

The term "IBM Q" has been used in some promotional material as of 2020, e.g.: www.ibm.com/mysupport/s/topic/0TO50000000227pGAA/ibm-q-quantum-computing?language=en_US though the fuller form "IBM Quantum Computing" is somewhat more widely used.

They also internally named an division as "IBM Q": sg.news.yahoo.com/ibm-thinks-ready-turn-quantum-050100574.html

IBM quantum computer

IQM

Words: 1

Homepage: meetiqm.com/

OpenSuperQ

Words: 13

Open source superconducting quantum computer hardware design!

Video 26.

OpenSuperQ intro by Quantum Flagship (2021)

Source.

youtu.be/2cU2PA4Q0Bw?t=61: Dilution refrigerator by Bluefors

Oxford Quantum Circuits (2017, OQC)

Words: 126 Articles: 1

oxfordquantumcircuits.com/

Their main innovation seems to be their 3D design which they call "Coaxmon".

Funding:

2023: $1m (869,000 pounds) for Japan expansion: www.uktech.news/deep-tech/oqc-funding-japan-20230203
2022: $47m (38M pounds) techcrunch.com/2022/07/04/uks-oxford-quantum-circuits-snaps-up-47m-for-quantum-computing-as-a-service/
2017: $2.7m globalventuring.com/university/oxford-quantum-calculates-2-7m/

Video 27.

The Coaxmon by Oxford Quantum Circuits (2022)

Source.

Ilana Wisby

Words: 96

Founding CEO of Oxford Quantum Circuits.

As mentioned at www.investmentmonitor.ai/tech/innovation/in-conversation-with-oxford-quantum-circuits-ilana-wisby she is not the original tech person:

she was finally headhunted by Oxford Science and Innovation to become the founding CEO of OQC. The company was spun out of Oxford University's physics department in 2017, at which point Wisby was handed "a laptop and a patent".

Did they mean Oxford Sciences Enterprises? There's nothing called "Oxford Science and Innovation" on Google. Yes, it is just a typo oxfordscienceenterprises.com/news/meet-the-founder-ilana-wisby-ceo-of-oxford-quantum-circuits/ says it clearly:

I was headhunted by Oxford Sciences Enterprises to be the founding CEO of OQC.

oxfordquantumcircuits.com/story mentions that the core patent was by Dr. Peter Leek: www.linkedin.com/in/peter-leek-00954b62/

Rigetti Computing (2017, OQC)

Words: 45

Video 28.

Forest: an Operating System for Quantum Computing by Guen Prawiroatmodjo (2017)

Source. The title of the talk is innapropriate, this is a very basic overview of the entire Rigetti Computing stack. Still some fine mentions. Her name is so long, TODO origin? She later moved to Microsoft Quantum: www.linkedin.com/in/gueneverep/.

Topological quantum computer

Words: 19

Video 29.

Topological Quantum Computer by Professor John Preskill

. Source.

Video 30.

Topological Quantum Computation by Jason Alicea (2021)

Source.

Video 31.

Anyons by Yuly Billig (2022)

Source.

Trapped ion quantum computer

Words: 2k Articles: 15

TODO understand.

Video 32.

Trapping Ions for Quantum Computing by Diana Craik (2019)

Source.

A basic introduction, but very concrete, with only a bit of math it might be amazing:

youtu.be/j1SKprQIkyE?t=217 you need ultra-high vacuum
youtu.be/j1SKprQIkyE?t=257 you put the Calcium on a "calcium oven", heat it up, and make it evaporates a little bit
youtu.be/j1SKprQIkyE?t=289 you need lasers. You shine the laser on the calcium atom to eject one of the two valence electrons from it. Though e.g. Universal Quantum is trying to do away with them, because alignment for thousands or millions of particles would be difficult.
youtu.be/j1SKprQIkyE?t=518 keeping all surrounding electrodes positive would be unstable. So they instead alternate electrode quickly between plus and minus
youtu.be/j1SKprQIkyE?t=643 talks about the alternative, of doing it just with electrodes on a chip, which is easier to manufacture. They fly at about 100 microns above the trap. And you can have multiple ions per chip.
youtu.be/j1SKprQIkyE?t=1165 using microwaves you can flip the spin of the electron, or put it into a superposition. From more reading, we understand that she is talking about a hyperfine transition, which often happen in the microwave area.
youtu.be/j1SKprQIkyE?t=1210 talks about making quantum gates. You have to put the ions into a magnetic field at one of the two resonance frequencies of the system. Presumably what is meant is an inhomogenous magnetic field as in the Stern-Gerlach experiment.
This is the hard and interesting part. It is not clear why the atoms become coupled in any way. Is it due to electric repulsion?
She is presumably describing the Cirac–Zoller CNOT gate.

Sounds complicated, several technologies need to work together for that to work! Videos of ions moving are from www.physics.ox.ac.uk/research/group/ion-trap-quantum-computing.

A major flaw of this presentation is not explaining the readout process.

Video 33.

How To Trap Particles in a Particle Accelerator by the Royal Institution (2016)

Source. Demonstrates trapping pollen particles in an alternating field.

Video 34.

Ion trapping and quantum gates by Wolfgang Ketterle (2013)

Source.

youtu.be/lJOuPmI--5c?t=1601 Cirac–Zoller CNOT gate was the first 2 qubit gate. Explains it more or less.

Video 35.

Introduction to quantum optics by Peter Zoller (2018)

Source. THE Zoller from Cirac–Zoller CNOT gate talks about his gate.

www.youtube.com/watch?v=W3l0QPEnaq0&t=427s shows that the state is split between two options: center of mass mode (ions move in same direction), and strechmode (atoms move in opposite directions)
youtu.be/W3l0QPEnaq0?t=658 shows a schematic of the experiment

Cirac–Zoller controlled-NOT gate (1995)

Ion trap

Modular trapped ion quantum computer

Words: 55

Trapped ion people acknowledge that they can't put a million qubits in on chip (TODO why) so they are already thinking of ways to entangle separate chips. Thinking is maybe the key word here. One of the propoesd approaches inolves optical links. Universal Quantum for example explicitly rejects that idea in favor of electric field link modularity.

Organization developing trapped ion quantum computer

Words: 1k Articles: 11

IonQ (2015)

Words: 497

Video 36.

Quantum Simulation and Computation with Trapped Ions by Christopher Monroe (2021)

Source.

Video 37.

Quantum Computing with Trapped Ions by Christopher Monroe (2018)

Source. Co-founder of IonQ. Cool dude. Starts with basic background we already know now. Mentions that there is some relationship between atomic clocks and trapped ion quantum computers, which is interesting. Then he goes into turbo mode, and you get lost unless you're an expert! Video 36. "Quantum Simulation and Computation with Trapped Ions by Christopher Monroe (2021)" is perhaps a better watch.

youtu.be/9aOLwjUZLm0?t=1216 superconducting qubits are bad because it is harder to ensure that they are all the same
youtu.be/9aOLwjUZLm0?t=1270 our wires are provided by lasers. Gives example of ytterbium $^{+ 1}$ , which has nice frequencies for practical laser choice. Ytterbium ends in 6s2 5d1, so they must remove the 5d1 electron? But then you are left with 2 electrons in 6s2, can you just change their spins at will without problem?
youtu.be/9aOLwjUZLm0?t=1391 a single atom actually reflects 1% of the input laser, not bad!
youtu.be/9aOLwjUZLm0?t=1475 a transition that they want to drive in Ytterbium has 355 nm, which is easy to generate TODO why.
youtu.be/9aOLwjUZLm0?t=1520 mentions that 351 would be much harder, e.g. as used in inertially confied fusion, takes up a room
youtu.be/9aOLwjUZLm0?t=1539 what they use: a pulsed laser. It is made primarily for photolithography, Coherent, Inc. makes 200 of them a year, so it is reliable stuff and easy to operate. At www.coherent.com/lasers/nanosecond/avia-nx we can see some of their 355 offers. archive.ph/wip/JKuHI shows a used system going for 4500 USD.
youtu.be/9aOLwjUZLm0?t=1584 Cirac and Zoller proposed the idea of using entangled ions soon after they heard about Shor's algorithm in 1995
youtu.be/9aOLwjUZLm0?t=1641 you use optical tweezers to move the pairs of ions you want to entangle. This means shining a laser on two ions at the same time. Their movement depends on their spin, which is already in a superposition. If both move up, their distance stats the same, so the Coulomb interaction is unchanged. But if they are different, then one goes up and the other down, distance increases due to the diagonal, and energy is lower.
youtu.be/9aOLwjUZLm0?t=1939 S. Debnah 2016 Nature experiment with a pentagon. Well, it is not a pentagon, they are just in a linear chain, the pentagon is just to convey the full connectivity. Maybe also Satanism. Anyways. This point also mentions usage of an acousto-optic modulator to select which atoms we want to act on. On the other side, a simpler wide laser is used that hits all atoms (optical tweezers are literally like tweezers in the sense that you use two lasers). Later on mentions that the modulator is from Harris, later merged with L3, so: www.l3harris.com/all-capabilities/acousto-optic-solutions
youtu.be/9aOLwjUZLm0?t=2119 Bernstein-Vazirani algorithm. This to illustrate better connectivity of their ion approach compared to an IBM quantum computer, which is a superconducting quantum computer
youtu.be/9aOLwjUZLm0?t=2354 hidden shift algorithm
youtu.be/9aOLwjUZLm0?t=2740 Zhang et al. Nature 2017 paper about a 53 ion system that calculates something that cannot be classically calculated. Not fully controllable though, so more of a continuous-variable quantum information operation.
youtu.be/9aOLwjUZLm0?t=2923 usage of cooling to 4 K to get lower pressures on top of vacuum. Before this point all experiments were room temperature. Shows image of refrigerator labelled Janis cooler, presumably something like: qd-uki.co.uk/cryogenics/janis-recirculating-gas-coolers/
youtu.be/9aOLwjUZLm0?t=2962 qubit vs gates plot by H. Neven
youtu.be/9aOLwjUZLm0?t=3108 modular trapped ion quantum computer ideas. Mentions experiment with 2 separate systems with optical link. Miniaturization and their black box. Mentions again that their chip is from Sandia. Amazing how you pronounce that.

NQIT

Words: 28

Video 38.

Quantum Computing with Networked Ion traps by NQIT (2018)

Source. The video is a bit useless. But it does show the networked approach proposal a little bit. Universal Quantum's homepage particularly rejects that.

Oxford Ionics (2017, OQC)

Words: 21

This job announcement from 2022 gives a good idea about their tech stack: web.archive.org/web/20220920114810/https://oxfordionics.bamboohr.com/jobs/view.php?id=32&source=aWQ9MTA%3D. Notably, they use ARTIQ.

Funding:

2023: $36m www.forbes.com/sites/gilpress/2023/01/09/36-million-oxford-ionics-funding-to-jump-start-quantum-computing-in-2023/?sh=6af75e7a6ccb

Quantinuum

Words: 58 Articles: 6

Merger between Cambridge Quantum Computing, which does quantum software, and Honeywell Quantum Solutions, which does the hardware.

Quantinuum hardware

Words: 3 Articles: 2

Quantinuum H1

Quantinuum H1-2

Words: 3

E.g.: www.quantinuum.com/pressrelease/demonstrating-benefits-of-quantum-upgradable-design-strategy-system-model-h1-2-first-to-prove-2-048-quantum-volume from 2021.

Cambridge Quantum Computing

Words: 43 Articles: 1

In 2015, they got a 50 million investment from Grupo Arcano, led by Alberto Chang-Rajii, who is a really shady character who fled from justice for 2 years:

Merged into Quantinuum later on in 2021.

tket

Words: 5

github.com/CQCL/tket

TODO vs all the others?

Honeywell Quantum Solutions

Universal Quantum

Words: 546

As of 2021, their location is a small business park in Haywards Heath, about 15 minutes north of Brighton ^[ref]

Funding rounds:

2022:
- 67m euro contract with the German government: www.uktech.news/deep-tech/universal-quantum-german-contract-20221102 Both co-founders are German. They then immediatly announced several jobs in Hamburg: apply.workable.com/universalquantum/?lng=en#jobs so presumably linked to the Hamburg University of Technology campus of the German Aerospace Center.
- medium.com/@universalquantum/universal-quantum-wins-67m-contract-to-build-the-fully-scalable-trapped-ion-quantum-computer-16eba31b869e
2021: $10M (7.5M GBP) grant from the British Government: www.uktech.news/news/brighton-universal-quantum-wins-grant-20211105
This grant is very secretive, very hard to find any other information about it! Most investment trackers are not listing it.
The article reads:
Universal Quantum will lead a consortium that includes Rolls-Royce, quantum developer Riverlane, and world-class researchers from Imperial College London and The University of Sussex, among others.
Interesting!
A but further down the article gives some more information of partners, from which some of the hardware vendors can be deduced:
The consortium includes end-user Rolls-Royce supported by the Science and Technology Facilities Council (STFC) Hartree Centre, quantum software developer Riverlane, supply chain partners Edwards, TMD Technologies (now acquired by Communications & Power Industries (CPI)) and Diamond Microwave
- Edwards is presumably Edwards Vacuum, since we know that trapped ion quantum computers rely heavily on good vacuum systems. Edwards Vacuum is also located quite close to Universal Quantum as of 2022, a few minutes drive.
- TMD Technologies is a microwave technology vendor amongst other things, and we know that microwaves are used e.g. to initialize the spin states of the ions
- Diamond Microwave is another microwave stuff vendor
The money comes from UK's "Industrial Strategy Challenge Fund".
www.riverlane.com/news/2021/12/riverlane-joins-7-5-million-consortium-to-build-error-corrected-quantum-processor/ gives some more details on the use case provided by Rolls Royce:
The work with Rolls Royce will explore how quantum computers can develop practical applications toward the development of more sustainable and efficient jet engines.
This starts by applying quantum algorithms to take steps to toward a greater understanding of how liquids and gases flow, a field known as 'fluid dynamics'. Simulating such flows accurately is beyond the computational capacity of even the most powerful classical computers today.
This funding was part of a larger quantum push by the UKNQTP: www.ukri.org/news/50-million-in-funding-for-uk-quantum-industrial-projects/
2020: $4.5M (3.5M GBP) www.crunchbase.com/organization/universal-quantum. Just out of stealth.

Co-founders:

Sebastian Weidt. He is German, right? Yes at youtu.be/SwHaJXVYIeI?t=1078 from Video 41. "Fireside Chat with with Sebastian Weidt by Startup Grind Brighton (2022)". The company was founded by two Germans from Essex!
Winfried Hensinger: if you saw him on the street, you'd think he plays in a punk-rock band. That West Berlin feeling.

Homepage says only needs cooling to 70 K. So it doesn't work with liquid nitrogen which is 77 K?

Homepage points to foundational paper: www.science.org/doi/10.1126/sciadv.1601540

Video 39.

Universal Quantum emerges out of stealth by University of Sussex (2020)

Source. Explains that a more "traditional" trapped ion quantum computer would user "pairs of lasers", which would require a lot of lasers. Their approach is to try and do it by applying voltages to a microchip instead.

youtu.be/rYe9TXz35B8?t=127 shows some 3D models. It shows how piezoelectric actuators are used to align or misalign some plates, which presumably then determine conductivity

Video 40.

Quantum Computing webinar with Sebastian Weidt by Green Lemon Company (2020)

Source. The sound quality is to bad to stop and listen to, but it presumaby shows the coding office in the background.

Video 41.

Fireside Chat with with Sebastian Weidt by Startup Grind Brighton (2022)

Source. Very basic target audience:

youtu.be/SwHaJXVYIeI?t=680 we are not at a point where you can buy victory. There is too much uncertainty involved across different approaches.
youtu.be/SwHaJXVYIeI?t=949 his background
youtu.be/SwHaJXVYIeI?t=1277 difference between venture capitalists in different countries
youtu.be/SwHaJXVYIeI?t=1535 they are 33 people now. They've just setup their office in Haywards Heath, north of Bristol.

Neutral atom quantum computer

Words: 24 Articles: 4

quantumtech.blog/2023/01/17/quantum-computing-with-neutral-atoms/

Organization developing neutral atom quantum computer

Words: 24 Articles: 3

Atom Computing

Words: 21

These people are cool.

They use optical tweezers to place individual atoms floating in midair, and then do stuff to entangle their nuclear spins.

QuEra (2018)

Pasqal

Words: 3

pasqal.io/

Funding:

2023: $100m techcrunch.com/2023/01/23/pasqal-raises-100m-to-build-a-neutral-atom-based-quantum-computer/

Photonic quantum computer (Linear optical quantum computing)

Words: 424 Articles: 8

Uses photons!

The key experiment/phenomena that sets the basis for photonic quantum computing is the two photon interference experiment.

The physical representation of the information encoding is very easy to understand:

input: we choose to put or not photons into certain wires or no
interaction: two wires pass very nearby at some point, and photons travelling on either of them can jump to the other one and interact with the other photons
output: the probabilities that photos photons will go out through one wire or another

Video 42.

Jeremy O'Brien: "Quantum Technologies" by GoogleTechTalks (2014)

Source. This is a good introduction to a photonic quantum computer. Highly recommended.

youtube.com/watch?v=7wCBkAQYBZA&t=1285 shows an experimental curve for a two photon interference experiment by Hong, Ou, Mandel (1987)
youtube.com/watch?v=7wCBkAQYBZA&t=1440 shows a KLM CNOT gate
youtube.com/watch?v=7wCBkAQYBZA&t=2831 discusses the quantum error correction scheme for photonic QC based on the idea of the "Raussendorf unit cell"

Organization developing photonic quantum computer

Words: 295 Articles: 7

Quandela

Words: 32 Articles: 1

www.quandela.com

One interesting aspect of this company is that they are trying to sell not only full quantum computers, but also components that could be used by competitors, such as

Prometheus single photon source

Words: 4

www.quandela.com/prometheus/ (2024 archive)

ORCA Computing

Words: 9

www.orcacomputing.com/

2022: $15 million www.orcacomputing.com/blog/orca-computing-completes-15-million-series-a-funding-round
2021: $14.5 million for an Innovate UK project

PsiQuantum

Words: 228 Articles: 2

CEO: Jeremy O'Brien

Raised 215M in 2020: www.bloomberg.com/news/articles/2020-04-06/quantum-computing-startup-raises-215-million-for-faster-device

Good talk by CEO before starting the company which gives insight on what they are very likely doing: Video 42. "Jeremy O'Brien: "Quantum Technologies" by GoogleTechTalks (2014)"

PsiQuantum appears to be particularly secretive, even more than other startups in the field.

They want to reuse classical semiconductor fabrication technologies, notably they have close ties to GlobalFoundries.

So he went to the US and raised N times more from the American military-industrial complex.

Jeremy O'Brien

www.linkedin.com/in/jeremy-o-brien-39482631

PsiQuantum founding myth

Words: 162

Once upon a time, the British Government decided to invest some 80 million into quantum computing.

Jeremy O'Brien told his peers that he had the best tech, and that he should get it all.

Some well connected peers from well known universities did not agree however, and also bid for the money, and won.

Jeremy was defeated. And pissed.

So he moved to Palo Alto and raised a total of $665 million instead as of 2021. The end.

Makes for a reasonable the old man lost his horse.

www.ft.com/content/afc27836-9383-11e9-aea1-2b1d33ac3271 British quantum computing experts leave for Silicon Valley talks a little bit about them leaving, but nothing too juicy. They were called PsiQ previously apparently.

The departure of some of the UK’s leading experts in a potentially revolutionary new field of technology will raise fresh concerns over the country’s ability to develop industrial champions in the sector.

More interestingly, the article mentions that this was party advised by early investor Hermann Hauser, who is known to be preoccupied about UK's ability to create companies. Of course, European Tower of Babel.

Xanadu Quantum Technologies

Words: 26

Rounds:

2022-11: 100m USD www.prnewswire.com/news-releases/xanadu-closes-100m-usd-series-c-to-accelerate-development-of-fault-tolerant-quantum-computers-301672611.html

www.youtube.com/watch?v=v7iAqcFCTQQ shows their base technology:

laser beam comes in
input set via of optical ring resonators that form a squeezed state of light. Does not seem to rely on single photon production and detection experiments?

Quantum computing hardware bibliography

Words: 62 Articles: 2

Lists:

www.reddit.com/r/QuantumComputing/comments/j2rcbm/books_on_the_physical_design_of_quantum_computers/

Hardware for Quantum Computing by Chuck Easttom

Words: 61 Articles: 1

This book is mostly a failure unfortunately, as it glosses far too quickly over the physical implementations.

Chuck Easttom

Words: 44

Author of hardware for Quantum Computing by Chuck Easttom.

On Amazon: www.amazon.com/dp/3031664760

ISBN: 3031664760.

Certainly he looks after his image very strictly, endlessly saying how good he is. And he is definitely a high flying bird. Perhaps it is hard to differentiate genius from mad applies.

Video 43.

EC-Council Certified Encryption Specialist (ECES) with Chuck Easttom

. Source. Check saying how amazing he is.

Quantum interconnect

Words: 102 Articles: 2

"Quantum interconnect" refers to methods for linking up smaller quantum processors into a larger system.

As of 2024, seemingly few organizations developing quantum hardware had actually integrated multiple chips in interconnects as part of their main current roadmap. But many acknowledged that this would be an essential step towards scalable compuation.

The name "quantum interconnect" is likely partly a throwback to classical computer's "chip interconnect".

Sample usages of the term:

news.mit.edu/2023/quantum-interconnects-photon-emission-0105
Researchers have demonstrated directional photon emission, the first step toward extensible quantum interconnects
qpl.ece.ucsb.edu/research/quantum-interconnects

Video 44.

Gerhard Rempe - Quantum Dynamics by Max Planck Institute of Quantum Optics

. Source. No technical details of course, but they do show off their optical tables quite a bit!

Quantum interconnect company

Words: 4 Articles: 1

Welinq

Words: 4

Funding:

2023-01-23 €5 Million
- thequantuminsider.com/2023/01/23/welinq-closes-e5-million-pre-seed-round/

Quantum computer simulator

Words: 72

Other good lists:

quantumcomputingreport.com/resources/tools/ is hard to beat as usual.
www.quantiki.org/wiki/list-qc-simulators

JavaScript
- algassert.com/quirk demo: github.com/Strilanc/Quirk drag-and-drop, by a 2019-quantum-computing-Googler, impressive. You can create gates. State store in URL.
- github.com/stewdio/q.js/ demo: quantumjavascript.app/

Bibliography:

www.epcc.ed.ac.uk/whats-happening/articles/energy-efficient-quantum-computing-simulations mentions two types of quantum computer simulation:
- The most common approach to quantum simulations is to store the whole state in memory and to modify it with gates in a given order
- However, there is a completely different approach that can sometimes eliminate this issue - tensor networks

 Tagged

Qiskit Aer

Quantum software

Words: 951 Articles: 29

Quantum programming framework

Words: 669 Articles: 12

Cirq

PennyLane

Words: 10

By Xanadu.

Apparently meant to be higher level.

Homepage: pennylane.ai/

Source code: github.com/PennyLaneAI/pennylane

Qiskit

Words: 659 Articles: 9

Python library, claims multiple backends, including simulation and real IBM quantum computer.

Qiskit example

Words: 625 Articles: 4

Qiskit hello world

Words: 254 Articles: 1

The official hello world is documented at: qiskit.org/documentation/intro_tutorial1.html and contains a Bell state circuit.

Our version at qiskit/hello.py.

qiskit/hello.py

Words: 241

Our example uses a Bell state circuit to illustrate all the fundamental Qiskit basics.

Sample program output, counts are randomized each time.

First we take the quantum state vector immediately after the

∣ 00 ⟩

input.

input:
state:
Statevector([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
            dims=(2, 2))
probs:
[1. 0. 0. 0.]

We understand that the first element of Statevector is

∣ 00 ⟩

, and has probability of 1.0.

Next we take the state after a Hadamard gate on the first qubit:

h:
state:
Statevector([0.70710678+0.j, 0.70710678+0.j, 0.        +0.j,
             0.        +0.j],
            dims=(2, 2))
probs:
[0.5 0.5 0.  0. ]

We now understand that the second element of the Statevector is

∣ 01 ⟩

, and now we have a 50/50 propabability split for the first bit.

Then we apply the CNOT gate:

cx:
state:
Statevector([0.70710678+0.j, 0.        +0.j, 0.        +0.j,
             0.70710678+0.j],
            dims=(2, 2))
probs:
[0.5 0.  0.  0.5]

which leaves us with the final

\frac{∣ 00 ⟩ + ∣ 11 ⟩}{2}

Then we print the circuit a bit:

qc without measure:
     ┌───┐
q_0: ┤ H ├──■──
     └───┘┌─┴─┐
q_1: ─────┤ X ├
          └───┘
c: 2/══════════

qc with measure:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
qasm:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];

And finally we compile the circuit and do some sample measurements:

qct:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
counts={'11': 484, '00': 516}
counts={'11': 493, '00': 507}

qiskit/hello.py

#!/usr/bin/env python

from qiskit import QuantumCircuit, transpile
from qiskit_aer import Aer, AerSimulator
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_histogram

def print_state(qc):
    # Get state vector
    state = Aer.get_backend('statevector_simulator').run(qc, shots=1).result().get_statevector()
    print('state:')
    print(state)
    probs = state.probabilities()
    print('probs:')
    print(probs)

qc = QuantumCircuit(2, 2)
print('input:')
print_state(qc)
print()
qc.h(0)
print('h:')
print_state(qc)
print()
qc.cx(0, 1)
print('cx:')
print_state(qc)
print()
print('qc without measure:')
print(qc)

# Add measures and simulate some runs.
# Can't get state properly with measures.
qc.measure([0, 1], [0, 1])

# Print the circuit in a bunch of ways.
print('qc with measure:')
print(qc)
print('qasm:')
print(qc.qasm())
# Works but slows things down.
#qc.draw('mpl', filename='hello_qc.svg')

# Compile the circuit, and simulat it.
simulator = AerSimulator()
qct = transpile(qc, simulator)
# No changes in this specific case, as the simulator likely supports all gates.
print('qct:')
print(qct)
job = simulator.run(qc, shots=1000)
result = job.result()
counts = result.get_counts(qc)
print(f'{counts=}')
job = simulator.run(qc, shots=1000)
result = job.result()
counts = result.get_counts(qc)
print(f'{counts=}')
#plot_histogram(counts, filename='hello_hist.svg')

qiskit/initialize.py

Words: 170

In this example we will initialize a quantum circuit with a single CNOT gate and see the output values.

By default, Qiskit initializes every qubit to 0 as shown in the qiskit/hello.py. But we can also initialize to arbitrary values as would be done when computing the output for various different inputs.

Output:

     ┌──────────────────────┐
q_0: ┤0                     ├──■──
     │  Initialize(1,0,0,0) │┌─┴─┐
q_1: ┤1                     ├┤ X ├
     └──────────────────────┘└───┘
c: 2/═════════════════════════════

init: [1, 0, 0, 0]
probs: [1. 0. 0. 0.]

init: [0, 1, 0, 0]
probs: [0. 0. 0. 1.]

init: [0, 0, 1, 0]
probs: [0. 0. 1. 0.]

init: [0, 0, 0, 1]
probs: [0. 1. 0. 0.]

     ┌──────────────────────────────────┐
q_0: ┤0                                 ├──■──
     │  Initialize(0.70711,0,0,0.70711) │┌─┴─┐
q_1: ┤1                                 ├┤ X ├
     └──────────────────────────────────┘└───┘
c: 2/═════════════════════════════════════════

init: [0.7071067811865475, 0, 0, 0.7071067811865475]
probs: [0.5 0.5 0.  0. ]

which we should all be able to understand intuitively given our understanding of the CNOT gate and quantum state vectors.

quantumcomputing.stackexchange.com/questions/13202/qiskit-initializing-n-qubits-with-binary-values-0s-and-1s describes how to initialize circuits qubits only with binary 0 or 1 to avoid dealing with the exponential number of elements of the quantum state vector.

qiskit/qft.py

Words: 201

This is an example of the qiskit.circuit.library.QFT implementation of the Quantum Fourier transform function which is documented at: docs.quantum.ibm.com/api/qiskit/0.44/qiskit.circuit.library.QFT

Output:

init: [1, 0, 0, 0, 0, 0, 0, 0]
qc
     ┌──────────────────────────────┐┌──────┐
q_0: ┤0                             ├┤0     ├
     │                              ││      │
q_1: ┤1 Initialize(1,0,0,0,0,0,0,0) ├┤1 QFT ├
     │                              ││      │
q_2: ┤2                             ├┤2     ├
     └──────────────────────────────┘└──────┘
transpiled qc
     ┌──────────────────────────────┐                                     ┌───┐   
q_0: ┤0                             ├────────────────────■────────■───────┤ H ├─X─
     │                              │              ┌───┐ │        │P(π/2) └───┘ │ 
q_1: ┤1 Initialize(1,0,0,0,0,0,0,0) ├──────■───────┤ H ├─┼────────■─────────────┼─
     │                              │┌───┐ │P(π/2) └───┘ │P(π/4)                │ 
q_2: ┤2                             ├┤ H ├─■─────────────■──────────────────────X─
     └──────────────────────────────┘└───┘
Statevector([0.35355339+0.j, 0.35355339+0.j, 0.35355339+0.j,
             0.35355339+0.j, 0.35355339+0.j, 0.35355339+0.j,
             0.35355339+0.j, 0.35355339+0.j],
            dims=(2, 2, 2))

init: [0.0, 0.35355339059327373, 0.5, 0.3535533905932738, 6.123233995736766e-17, -0.35355339059327373, -0.5, -0.35355339059327384]
Statevector([ 7.71600526e-17+5.22650714e-17j,
              1.86749130e-16+7.07106781e-01j,
             -6.10667421e-18+6.10667421e-18j,
              1.13711443e-16-1.11022302e-16j,
              2.16489014e-17-8.96726857e-18j,
             -5.68557215e-17-1.11022302e-16j,
             -6.10667421e-18-4.94044770e-17j,
             -3.30200457e-16-7.07106781e-01j],
            dims=(2, 2, 2))

So this also serves as a more interesting example of quantum compilation, mapping the QFT gate to Qiskit Aer primitives.

If we don't transpile in this example, then running blows up with:

qiskit_aer.aererror.AerError: 'unknown instruction: QFT'

The second input is:

x_{i} = \frac{1}{2} s in (2 * π * i /8)

(19)

and the output of that approximately:

[0, 1j/sqrt(2), 0, 0, 0, 0, 0, 1j/sqrt(2)]

which can be defined simply as the normalized DFT of the input quantum state vector.

From this we see that the Quantum Fourier transform is equivalent to a direct discrete Fourier transform on the quantum state vector, related: physics.stackexchange.com/questions/110073/how-to-derive-quantum-fourier-transform-from-discrete-fourier-transform-dft

qiskit/qft.py

#!/usr/bin/env python

import math

from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import QFT
from qiskit_aer import Aer, AerSimulator

n = 3
N = 2**n

def test(init, print_qc=False):
    qc = QuantumCircuit(n)
    qc.initialize(init)
    qft = QFT(num_qubits=n).to_gate()
    qc.append(qft, qargs=range(3))
    print(f'init: {init}')
    if print_qc:
        print('qc')
        print(qc)
    qc = transpile(qc, AerSimulator())
    if print_qc:
        print('transpiled qc')
        print(qc)
    print(Aer.get_backend('statevector_simulator').run(qc, shots=1).result().get_statevector())
    print()

test([1] + [0] * (N - 1), print_qc=True)
test([math.sin(i * 2 * math.pi / N)/2 for i in range(N)])

Qiskit component

Words: 25 Articles: 3

`qiskit.transpile()`

Words: 8

This function does quantum compilation. Shown e.g. at qiskit/qft.py.

Qiskit Aer

Words: 17 Articles: 1

github.com/Qiskit/qiskit-aer

AerError: 'unknown instruction

Words: 17

You get an error like this if you forget to call qiskit.transpile():

qiskit_aer.aererror.AerError: 'unknown instruction: QFT'

Quantum circuit description language

Words: 58

These are a bit like the Verilog of quantum computing.

One would hope that they are not Turing complete, this way they may serve as a way to pass on data in such a way that the receiver knows they will only be doing so much computation in advance to unpack the circuit. So it would be like JSON is for JavaScript.

OpenQASM

Words: 32

On Qiskit qiskit==0.44.1:

qc.qasm()

E.g. with our qiskit/hello.py, we obtain the Bell state circuit:

OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];

Quantum control system

Words: 192 Articles: 13

Some people call it "operating System".

The main parts of those systems are:

sending multiple signals at very precise times to the system
reading out some quantum error correction bits and sending error correcting signals back in a control loop

Quantum control systems use FPGAs

Words: 39

It seems that all/almost all of them do. Quite cool.

Video 45.

FPGA Architecture of the Quantum Control System by Keysight (2022)

Source. They actually have a dedicated quantum team! Cool.

Video 46.

FPGA based servo system by Atoms & Laser (2018)

Source. The Indian lady is hardcore.

Organization developing quantum control systems

Words: 110 Articles: 9

github.com/m-labs/artiq

M-Labs

Articles: 2

ARTIQ

Articles: 1

Duke ARTIQ extensions

gitlab.com/duke-artiq/dax

Q-CTRL

Words: 11

q-ctrl.com/

Someone attempted a Wikipedia page apparently: en.wikipedia.org/wiki/Q-CTRL. Nice try, nice try.

QuantrolOx

q-ctrl.com/

Quantum Machines

Riverlane (2017)

Words: 99 Articles: 1

www.riverlane.com/

When you fail a HR interview, then you know you've reached rock bottom.

Investments:

2024: 75m GBP
2023-04: 15m GBP: www.uktech.news/deep-tech/riverlane-series-b-20230424 At 100 employeed on LinkedIn, this should keep them going for two more years.
2022 500k GBP: www.uktech.news/deep-tech/riverlane-rigetti-quantum-innovate-uk-20220628 by Innovate UK for joing project with Rigetti Computing to work on quantum error correction

Video 47.

The Operating System for Quantum Computing by Steve Brierley (2021)

Source. Founding CEO. He seems nice. You might as well just start watching at: youtu.be/ugzWnw1LTBE?t=1166 where more specific things start to come out.

Deltaflow.OS

Words: 23

A "quantum computer operating system". Or in English, control system + quantum error correction.

uknqt.ukri.org/wp-content/uploads/2021/10/UKNQTP-Strategic-Intent-2020.pdf page 24 mentions UKNQTP investment and gives an overview of some layers.

Zurich Instruments

www.zhinst.com/europe/en/quantum-computing-systems/qccs

List of quantum control systems

Words: 6 Articles: 1

 Tagged

ARTIQ

Pulser (quantum control)

Words: 6

github.com/pasqal-io/Pulser

This is the one by Pasqal.

Classical computer

Words: 21

In the context of quantum computing of the 2020's, a "classical computer" is a computer that is not "quantum", i.e., the then dominating CMOS computers.

ZX-calculus

Words: 281 Articles: 3

As en.wikipedia.org/w/index.php?title=ZX-calculus&oldid=1071329204#Diagram_rewriting tries to explain but fails to deliver as usual consider the GHZ state represented as a quantum circuit.

How can we easily prove that that quantum circuit equals the state:

\frac{∣000 > + ∣111 >}{2}

(20)

The naive way would be to just do the matrix multiplication as explained at Section "Quantum computing is just matrix multiplication".

However, ZX-calculus provides a simpler way.

And even more importantly, sometimes it is the only way, because in a real circuit, we would not be able to do the matrix multiplication

What we do in ZX-calculus is we first transform the original quantum circuit into a ZX graph.

This is always possible, because we can describe how to do the conversion simply for any of the Clifford plus T gates, which is a set of universal quantum gates.

Then, after we do this transformation, we can start applying further transformations that simplify the circuit.

It has already been proven that there is no efficient algorithm for this (TODO source, someone said P-sharp complete best case)

But it has been proven in 2017 that any possible equivalence between quantum circuits can be reached by modifying ZX-calculus circuits.

There are only 7 transformation rules that we need, and all others can be derived from those, universality.

So, we can apply those rules to do the transformation shown in Wikipedia:

Figure 10.
GHZ circuit as ZX-diagram
. Source.

and one of those rules finally tells us that that last graph means our desired state:

\frac{∣000 > + ∣111 >}{2}

(21)

because it is a Z spider with

m = 3

and

n = 1

Video 48.

Working with PyZX by Aleks Kissinger (2019)

Source. This video appears to give amazing motivation on why you should care about ZX-calculus, it mentions

quantum compilation
quantum computer simulation

Bibliography:

quantumcomputing.stackexchange.com/questions/9774/what-are-some-applications-of-the-zx-calculus
github.com/zxcalc/book Picturing Quantum Software by Aleks Kissinger and John van de Wetering (2024), CC BY-NC-SA.

 Tagged

ZX-calculus biliography

Words: 2 Articles: 1

Picturing Quantum Processes (2017)

Words: 2

PyZX

github.com/Quantomatic/pyzx

Quantum state

Words: 242 Articles: 4

Bell state

Words: 227 Articles: 1

One of the four following states:

∣ Φ^{+} ⟩ = \frac{1}{2} (∣ 00 ⟩ + ∣ 11 ⟩) ∣ Φ^{-} ⟩ = \frac{1}{2} (∣ 00 ⟩ - ∣ 11 ⟩) ∣ Ψ^{+} ⟩ = \frac{1}{2} (∣ 01 ⟩ + ∣ 10 ⟩) ∣ Ψ^{-} ⟩ = \frac{1}{2} (∣ 01 ⟩ - ∣ 10 ⟩)

(22)

When unqualified as in "the Bell state", it generally just means

∣ Φ^{+} ⟩

The Bell states are entangled and non-separable. Intuitively, we can see that when we measure that state, the values of the first and second bit are strictly correlated. This is the hallmark of quantum computation: making up states where qubits are highly correlated to match a specific algorithmic answer, and opposed to uniformly random noise. For example, the Bell state circuit is a common hello world, e.g. it is used in the official Qiskit hello world.

Bell circuit

Words: 113

A quantum circuit which when fed with input

∣ 00 ⟩

produces the Bell state.

In Qiskit at: qiskit/hello.py.

Figure 11.
Quantum circuit that generates the Bell state
. Source.
The fundamental intuition for this circuit is as follows.
First the Hadamard gate makes the first qubit be in a 50/50 state.
Then, the CNOT gate gets controlled by that 50/50 value, and the controlled qubit also gets 50/50 chance as a result.
However, both qubits are now entangled: the result of the second qubit depends on the result of the first one. Because:
if the first qubit is 0, cnot is not active, and so the second qubit remains 0 as its input
if the first qubit is 1, cnot is active, and so the second qubit is flipped to 1

Greenberger-Horne-Zeilinger state

Quantum memory

Words: 15

TODO clear example and application.

www.quantamagazine.org/quantum-memory-proves-exponentially-powerful-20241016/ from Quanta Magazine has an incomprehensible news of something that sounds cool

Quantum supremacy (2019)

Words: 36 Articles: 2

Google's 2019 quantum supremacy claim

Quantum advantage

Words: 36

Similar to quantum supremacy, but add the goal that the computation must be useful, i.e. make money or solve some open mathematical problem, Ciro Santilli's wife was quite excited about the possibility of finding some counter examples in number theory with quantum computers.

Qubit

Quantum computer benchmark

Words: 300 Articles: 6

One important area of research and development of quantum computing is the development of benchmarks that allow us to compare different quantum computers to decide which one is more powerful than the other.

Ideally, we would like to be able to have a single number that predicts which computer is more powerful than the other for a wide range of algorithms.

However, much like in CPU benchmarking, this is a very complex problem, since different algorithms might perform differently in different architectures, making it very hard to sum up the architecture's capabilities to a single number as we would like.

The only thing that is directly comparable across computers is how two machines perform for a single algorithm, but we want a single number that is representative of many algorithms.

For example, the number of qubits would be a simple naive choice of such performance predictor number. But it is very imprecise, since other factors are also very important:

qubit error rate
coherence time, which determines the maximum circuit depth
qubit connectivity. Can you only connect to 4 neighbouring qubits in a 2D plane? Or to every other qubit equally as well?

Quantum volume is another less naive attempt at such metric.

Comparison of quantum computing hardware

Words: 39

System	Announcement date	Type	Qubits	Average connectivity	Coherence time	Measurements per second	Single qubit error	CZ error
Willow	2024-12	superconducting	105^[ref]	3.47^[ref]	68 μs^[ref]	63 k^[ref]	0.035%^[ref]	0.33%^[ref]

Other comparisons:

terra-docs.s3.us-east-2.amazonaws.com/IJHSR/Articles/volume6-issue8/IJHSR_2024_68_52.pdf Comparison Between Different Qubit Designs for Quantum Computing by Zaichen Hao (2024)

Algorithmic qubits

Words: 4

Metric created by IonQ.

Coherence time

Words: 21

It takes time for the quantum state to evolve. So in order to have a deep quantum circuit, we need longer coherence times.

Depth of a quantum circuit

Words: 40

This is an important metric, because it takes some time for the quantum operations to propagate, and so the depth of a circuit gives you an idea of how long the coherence time a hardware needs to support a given circuit.

Bibliography:

Quantum volume

Random circuit sampling

quantumcomputing.stackexchange.com/questions/4005/what-exactly-is-random-circuit-sampling

Quantum computing market

Articles: 2

Quantum computing skepticism

Articles: 1

Are we in a quantum computing bubble?

www.reddit.com/r/QuantumComputing/comments/lf1vp2/comment/ibuukcq/?utm_source=reddit&utm_medium=web2x&context=3

Post-quantum cryptography (PQC)

Words: 372 Articles: 6

Encryption algorithms that run on classical computers that are expected to be resistant to quantum computers.

This is notably not the case of the dominant 2020 algorithms, RSA and elliptic curve cryptography, which are provably broken by Grover's algorithm.

However, as of 2020, we don't have any proof that any symmetric or public key algorithm is quantum resistant.

Post-quantum cryptography is the very first quantum computing thing at which people have to put money into.

The reason is that attackers would be able to store captured ciphertext, and then retroactively break them once and if quantum computing power becomes available in the future.

There isn't a shade of a doubt that intelligence agencies are actively doing this as of 2020. They must have a database of how interesting a given source is, and then store as much as they can given some ammount of storage budget they have available.

A good way to explain this to quantum computing skeptics is to ask them:

If I told you there is a 5% chance that I will be able to decrypt everything you write online starting today in 10 years. Would you give me a dollar to reduce that chance to 0.5%?

Post-quantum cryptography is simply not a choice. It must be done now. Even if the risk is low, the cost would be way too great.

Post-quantum cryptography company

Words: 31 Articles: 1

PQShield (2018)

Words: 31

They seem to be doing hardware acceleration for post-quantum cryptography algorithm.

One has to feel bad for them as they likely threw out entire chip designs over NIST Post-Quantum Cryptography Standardization algorithm breakeges.

NIST Post-Quantum Cryptography Standardization (2017-)

Words: 111

This post-quantum cryptography competition by NIST is a huge milestone of the field.

It was mind blowing when in 2022, after several years of selection, one of the 7 finalists was broken on a classical computer, not even in a quantum computer! news.ycombinator.com/item?id=30466063 | eprint.iacr.org/2022/214 Breaking Rainbow Takes a Weekend on a Laptop by Ward Beullens. Dude announced he had a break a few days before submission: twitter.com/WardBeullens/status/1492780462028300290 On Twitter. He's so young. Epic.

Edit: and then, after the third round, things were a bit unclear, so they made a fourth round with 4 choices out of the 7 from round 3, and in August 2022 one of the four was broken again on a classic CPU!!! OMG: arstechnica.com/information-technology/2022/08/sike-once-a-post-quantum-encryption-contender-is-koed-in-nist-smackdown/

Provably quantum secure encryption algorithm

Words: 5

None known as of 2020.

Quantum resistant cryptosystem

Words: 15 Articles: 1

 Tagged

Is AES quantum resistant?

Lattice-based cryptography

Words: 15

Bibliography:

on Quanta Magazine: www.quantamagazine.org/cryptographys-future-will-be-quantum-safe-heres-how-it-will-work-20221109/ "Cryptography’s Future Will Be Quantum-Safe. Here’s How It Will Work." (2024)

Quantum computing outreach

Words: 37 Articles: 1

qosf.org
www.qubitbyqubit.org/
www.qsium.com/
Qsium is a student-led initiative that aims to democratise education in quantum computing. With the focus of raising 'quantum literacy' and creating a thriving quantum ecosystem through our Quantum Youth Network, we support STEM students in the UK.
qworld.net

 Tagged