Ciro Santilli
OurBigBook.comThe proper precise definition of mathematics can be found at: Section "Formalization of mathematics".
The most beautiful things in mathematics are described at: Section "The beauty of mathematics".
Study Hilbert spaces desert dilemma meme
. Source. Applies to almost all of mathematics of course. But we don't care, do we!Ciro Santilli intends to move his beauty list here little by little: github.com/cirosantilli/mathematics/blob/master/beauty.md
The most beautiful things in mathematics are results that are:
- simple to state but hard to prove:
- Fermat's Last Theorem
- number of unknown rationality, e.g. is rational?
- transcendental number conjectures, e.g. is transcendental?
- basically any conjecture involving prime numbers:
- many combinatorial game questions, e.g.:
- surprising results: we had intuitive reasons to believe something as possible or not, but a theorem shatters that conviction and brings us on our knees, sometimes via pathological counter-examples. General surprise themes include:Lists:
- classification of potentially infinite sets like: compact manifolds, etc.
- problems that are more complicated in low dimensions than high like:
- generalized Poincaré conjectures. It is also fun to see how in many cases complexity peaks out at 4 dimensions.
- classification of regular polytopes
- unpredictable magic constants:
- why is the lowest dimension for an exotic sphere 7?
- why is 4 the largest degree of an equation with explicit solution? Abel-Ruffini theorem
- undecidable problems, especially simple to state ones:
- mortal matrix problem
- sharp frontiers between solvable and unsolvable are also cool:
- attempts at determining specific values of the Busy beaver function for Turing machines with a given number of states and symbols
- related to Diophantine equations:
- applications: make life easier and/or modeling some phenomena well, e.g. in physics. See also: explain how to make money with the lesson
Good lists of such problems Lists of mathematical problems.
Whenever Ciro Santilli learns a bit of mathematics, he always wonders to himself:Unfortunately, due to how man books are written, it is not really possible to reach insight without first doing a bit of memorization. The better the book, the more insight is spread out, and less you have to learn before reaching each insight.
Am I achieving insight, or am I just memorizing definitions?
Tagged
One of the most beautiful things in mathematics are theorems of conjectures that are very simple to state and understand (e.g. for K-12, lower undergrad levels), but extremely hard to prove.
This is in contrast to conjectures in certain areas where you'd have to study for a few months just to precisely understand all the definitions and the interest of the problem statement.
Bibliography:
- mathoverflow.net/questions/75698/examples-of-seemingly-elementary-problems-that-are-hard-to-solve
- www.reddit.com/r/mathematics/comments/klev7b/whats_your_favorite_easy_to_state_and_understand/
- mathoverflow.net/questions/42512/awfully-sophisticated-proof-for-simple-facts this one is for proofs for which simpler proofs exist
- math.stackexchange.com/questions/415365/it-looks-straightforward-but-actually-it-isnt this one is for "there is some reason it looks easy", whatever that means
A beautiful quote fom Edward Titchmarsh:[ref]Ciro Santilli believes that it is perhaps for this reason that simple to state but hard to prove theorems are so attractive.
It can be of no practical use to know that pi is irrational, but if we can know, it surely would be intolerable not to know.
This quote was brought to Ciro Santilli's attention at: www.quantamagazine.org/recounting-the-history-of-maths-transcendental-numbers-20230627/
Randomly reproduced at: web.archive.org/web/20080105074243/http://personal.stevens.edu/~nkahl/Top100Theorems.html
In mathematics, a "classification" means making a list of all possible objects of a given type.
Classification results are some of Ciro Santilli's favorite: Section "The beauty of mathematics".
Examples:
- classification of finite simple groups
- classification of regular polytopes
- classification of closed surfaces, and more generalized generalized Poincaré conjectures
- classification of associative real division algebras
- classification of finite fields
- classification of simple Lie groups
- classification of the wallpaper groups and the space groups
Tagged
Oh, and the dude who created the en.wikipedia.org/wiki/Exceptional_object Wikipedia page won an Oscar: www.youtube.com/watch?v=oF_FLN-TmCY, Dan Piponi, aka
@sigfpe. Cool dude.Cool examples:
Tagged
Good place to hunt for the beauty of mathematics.
He's a bit overly obsessed with polynomials for the taste of modern maths, but it's still fun.
Ciro Santilli would like to fully understand the statements and motivations of each the problems!
Easy to understand the motivation:
- Navier-Stokes existence and smoothness is basically the only problem that is really easy to understand the statement and motivation :-)
- p versus NP problem
Hard to understand the motivation!
- Riemann hypothesis: a bunch of results on prime numbers, and therefore possible applications to cryptographyOf course, everything of interest has already been proved conditionally on it, and the likely "true" result will in itself not have any immediate applications.As is often the case, the only usefulness would be possible new ideas from the proof technique, and people being more willing to prove stuff based on it without the risk of the hypothesis being false.
- Yang-Mills existence and mass gap: this one has to do with finding/proving the existence of a more decent formalization of quantum field theory that does not resort to tricks like perturbation theory and effective field theory with a random cutoff valueThis is important because the best theory of light and electrons (and therefore chemistry and material science) that we have today, quantum electrodynamics, is a quantum field theory.
Nice result on Lebesgue measurable required for uniqueness.
Definition: "easy" number theory learnt in primary school, notably the operations of addition, subtraction, multiplication and division.
Can be calculated efficiently with the Extended Euclidean algorithm.
math.stackexchange.com/questions/2382011/computational-complexity-of-modular-exponentiation-from-rosens-discrete-mathem mentions:can be calculated in:Remember that and are the lengths in bits of and , so in terms of the length in bits and we'd get:
This section is about prime numbers that satisfy further properties beyond just being a prime.
There are infinitely many conjectures asking if such types of primes also form infinite families.
Usually the answer is yes, but no one was able to prove it yet.
Collaborative mega list: math.stackexchange.com/questions/4523193/are-there-infinitely-many-primes-of-the-form-x-we-probably-dont-know
Good section also at: en.wikipedia.org/wiki/List_of_unsolved_problems_in_mathematics#Prime_numbers
There are infinitely many prime k-tuples for every admissible tuple.
Generalization of the Twin prime conjecture.
As of 2023, there was no specific admissible tuple for which it had been proven that there infinite of, only bounds of type:But these do not specify which specific tuple, e.g. Yitang Zhang's theorem.
there are infinitely 2-tuple instances with at most a finite bound
Tagged
There are infinitely many primes with a neighbor not further apart than 70 million. This was the first such finite bound to be proven, and therefore a major breakthrough.
This implies that for at least one value (or more) below 70 million there are infinitely many repetitions, but we don't know which e.g. we could have infinitely many:or infinitely many:or infinitely many:or infinitely many:but we don't know which of those.
The Prime k-tuple conjecture conjectures that it is all of them.
Also, if 70 million could be reduced down to 2, we would have a proof of the Twin prime conjecture, but this method would only work for (k, k + 2).
Let's show them how it's done with primes + awk. Edit. They have a gives us the list of all twin primes up to 100:Tested on Ubuntu 22.10.
-d option which also shows gaps!!! Too strong:sudo apt install bsdgames
primes -d 1 100 | awk '/\(2\)/{print $1 - 2, $1 }'0 2
3 5
5 7
11 13
17 19
29 31
41 43
59 61
71 73 Tagged
Consider this is a study in failed computational number theory.
The approximation converges really slowly, and we can't easy go far enough to see that the ration converges to 1 with only awk and primes:Runs in 30 minutes tested on Ubuntu 22.10 and P51, producing:
sudo apt intsall bsdgames
cd prime-number-theorem
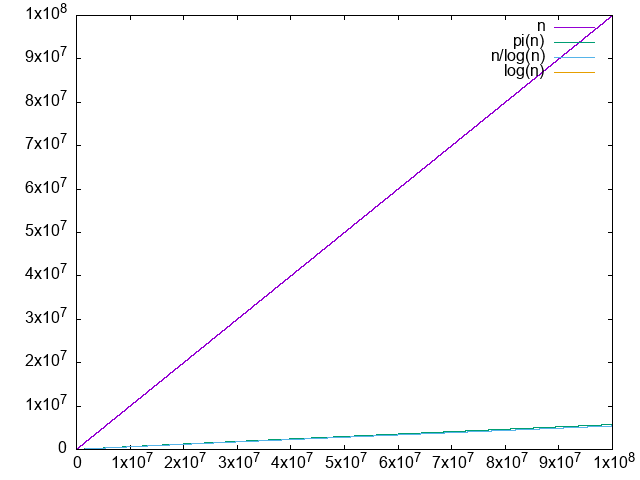
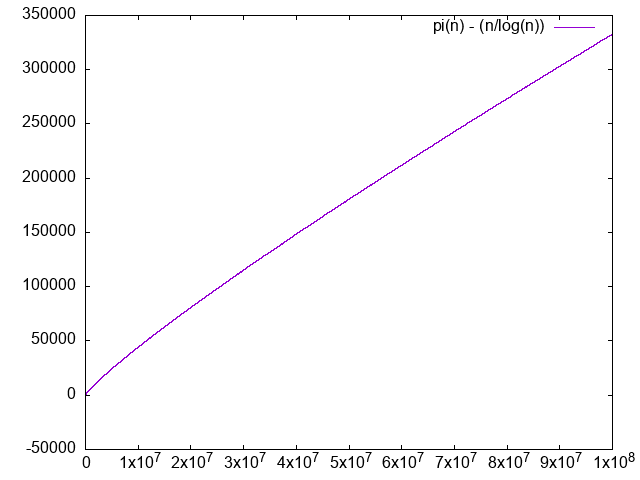
./main.py 100000000
Linear vs approximation plot
. and are added to give a better sense of scale. is too close to 0 and not visible, and the approximation almost overlaps entirely with .
. It is clear that the difference diverges, albeit very slowly.
. We just don't have enough points to clearly see that it is converging to 1.0, the convergence truly is very slow. The logarithm integral approximation is much much better, but we can't calculate it in awk, sadface.
But looking at: en.wikipedia.org/wiki/File:Prime_number_theorem_ratio_convergence.svg we see that it takes way longer to get closer to 1, even at it is still not super close. Inspecting the code there we see:so OK, it is not something doable on a personal computer just like that.
(* Supplement with larger known PrimePi values that are too large for \
Mathematica to compute *)
LargePiPrime = {{10^13, 346065536839}, {10^14, 3204941750802}, {10^15,
29844570422669}, {10^16, 279238341033925}, {10^17,
2623557157654233}, {10^18, 24739954287740860}, {10^19,
234057667276344607}, {10^20, 2220819602560918840}, {10^21,
21127269486018731928}, {10^22, 201467286689315906290}, {10^23,
1925320391606803968923}, {10^24, 18435599767349200867866}};They come up a lot in many contexts, e.g.:
Tagged
Polynomial time for most inputs, but not for some very rare ones. TODO can they be determined?
But it is better in practice than the AKS primality test, which is always polynomial time.
The "greatest common divisor" of two integers and , denoted is the largest natural number that divides both of the integers.
For example, is 4, because:
- 4 divides both 8 and 12
- and this is not the case for any number larger than 4. E.g.:and so on.
- 5 divides neither one
- 6 divides 12
- 7 divides neither
- 8 divides only 8
Two numbers such that the greatest common divisor is 1.
TODO wtf is a "totient"? Where else is that word used besides in this concept?
Techniques to get numerical approximations to numeric mathematical problems.
The entire field comes down to estimating the true values with a known error bound, and creating algorithms that make those error bounds asymptotically smaller.
Not the most beautiful field of pure mathematics, but fundamentally useful since we can't solve almost any useful equation without computers!
The solution visualizations can also provide valuable intuition however.
Important numerical analysis problems include solving:
Selected answers by Ciro Santilli on the subject:
All those dedicated applied mathematicians languages are a waste of society's time, Ciro Santilli sure applied mathematicians are capable of writing a few extra braces in exchange for a sane general purpose language, we should instead just invest in good libraries with fast C bindings for those languages like NumPy where needed, and powerful mainlined integrated development environments.
And when Ciro Santilli see the closed source ones like MATLAB being used, it makes him lose all hope on humanity. Why. As of 2020. Why? In the 1980s, maybe. But in the 2020s?
MATLAB Breaking Bad crossover
. Source. Used a lot in quantum mechanics, where the equations are really hard to solve. There's even a dedicated wiki page for it: en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics). Notably, Feynman diagrams are a way to represent perturbation calculations in quantum field theory.
Let's gather some of the best results we come across here:
A directed weighted graph where the sum of weights of all outgoing edges equals 1.
TODO how to calculate
TODO how to calculate
Tagged
Conditional probability by Art of the Problem
. Source. Tagged
Tagged
Under: graphviz.
graphviz/hello.dot
digraph {
top -> left;
top -> right;
left -> bottom;
right -> bottom;
}
graphviz/quotes.dot
digraph {
"My top" -> left;
"My top" -> right;
left -> "My bottom";
right -> "My bottom";
}
graphviz/node.dot
digraph {
top [ label = "My top" ];
bottom [ label = "My bottom" ];
top -> left;
top -> right;
left -> bottom;
right -> bottom;
}
graphviz/quotes-escape.dot
digraph {
"My \" top \\" -> left;
"My \" top \\" -> right;
left -> "My \" bottom \\";
right -> "My \" bottom \\";
}
A quick hands-on introduction to the software by Ciro Santilli can be found at: github.com/cirosantilli/cirosantilli.github.io/issues/198
The native file format of WebGraph.
It is a binary format and highly storage efficient.
It is for example what Common Crawl web graph currently dumps to as of 2025, see e.g.: data.commoncrawl.org/projects/hyperlinkgraph/cc-main-2024-25-dec-jan-feb/index.html
TODO meaning of "BV"?
A quick hands-on introduction to the format by Ciro Santilli can be found at: github.com/cirosantilli/cirosantilli.github.io/issues/198
This section is about ways in which you can represent a tree.
Trees are a specific type of graph, so any graph representation also provides a way to represent a tree.
Therefore this section will focus only on methods specific to tress, and which cannot be used for graphs in general.
This is particularly important in SQL: Nested set model in SQL, as it is an efficient way to transverse trees there, since querying parents every time would require multiple disk accesses.
The ASCII art visualizations from stackoverflow.com/questions/192220/what-is-the-most-efficient-elegant-way-to-parse-a-flat-table-into-a-tree/194031#194031 are worth reproducing.
As a tree:
- Root 1
- Child 1.1
- Child 1.1.1
- Child 1.1.2
- Child 1.2
- Child 1.2.1
- Child 1.2.2
- Child 1.1
As the sets:
__________________________________________________________________________
| Root 1 |
| ________________________________ ________________________________ |
| | Child 1.1 | | Child 1.2 | |
| | ___________ ___________ | | ___________ ___________ | |
| | | C 1.1.1 | | C 1.1.2 | | | | C 1.2.1 | | C 1.2.2 | | |
1 2 3___________4 5___________6 7 8 9___________10 11__________12 13 14
| |________________________________| |________________________________| |
|__________________________________________________________________________|Consider the following nested set:
0, 8, root
1, 7, mathematics
2, 3, geometry
3, 6, calculus
4, 5, derivative
5, 6, integral
6, 7, algebra
7, 8, physicsWhen we want to insert one element, e.g. so we have a method:
limit, normally under calculus, we have to specify:- parent
- index within parent
insert(parent, previousSibling) Tagged
Tagged
The summary from www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/ is a winner:
1
/ \
2 3
/ \
4 5- inorder DFS: 4 2 5 1 3
- preorder DFS: 1 2 4 5 3
- postorder DFS: 4 5 2 3 1
- breadth-first search: 1 2 3 4 5
In principle one could talk about tree traversal of unordered trees as a number of possible traversals without a fixed order. But we won't consider that under this section, only deterministic ordered tree traversals.
Tagged
This is the order in which you would want to transverse to read the chapters of a book.
Like breadth-first search, this also has the property of visiting parents before any children.
This is the easiest one to do iteratively:
- pop and visit
- push right to stack
- push left to stack
This is the order in which a binary search tree should be traversed for ordered output, i.e.:
- everything to the left is smaller than parent
- everything to the right is larger than parent
This ordering makes sense for binary trees and not k-ary trees in general because if there are more than two nodes it is not clear what the top node should go in the middle of.
This is unlike pre-order depth-first search and post-order depth-first search which generalize obviously to general trees.
This is a bit harder than iterative pre-order: now we have to check if there is a left or right element or not:
- (START) push current
- if there is left:
- move left
- else:
- (ELSE) pop
- visit
- if there is right
- move right
- GOTO START
- else:
- GOTO ELSE
The control flow can be slightly simplified if we allow NULLs: www.geeksforgeeks.org/inorder-tree-traversal-without-recursion/
Has the property of visiting all descendants before the parent.
This is the hardest one to do iteratively.
Bibliography:
Tagged
As mentioned at Human Compatible by Stuart J. Russell (2019), game theory can be seen as the part of artificial intelligence that deas with scenarios where multiple intelligent agents are involved.
Tagged
The best example to look at first is the penalty kick left right Nash equilibrium.
Then, a much more interesting example is choosing a deck of a TCG competition: Magic: The Gathering meta-based deck choice is a bimatrix game, which is the exact same, but each player has N choices rather than 2.
The next case that should be analyzed is the prisoner's dilemma.
The key idea is that:
- imagine that the game will be played many times between two players
- if one player always chooses one deck, the other player will adapt by choosing the anti-deck
- therefore, the best strategy for both players, is to pick decks randomly, each with a certain probability. This type of probabilistic approach is called a mixed strategy
- if any player deviates from the equilibrium probability, then the other player can add more of the anti-deck to the deck that the other player deviated, and gain an edgeTherefore, using equilibrium probabilities is the optimal way to play
When taking a penalty kick in soccer, the kicker must chose left or right.
And before he kicks, the goalkeeper must also decide left or right, because there is no time to see where the ball is going.
Because the kicker is right footed however, he kicker kicks better to one side than the other. So we have four probabilities:
- goal kick left keeper jumps left
- goal kick right keeper jumps right
- goal kick left keeper jumps right. Note that it is possible that this won't be a goal, even though the keeper is nowhere near the ball, as the ball might just miss the goal by a bit.
- kick right and keeper jumps left. Analogous to above
Related ideas:
Poet, scientists and warriors all in one? Conquerors of the useless.
A wise teacher from University of São Paulo once told the class Ciro Santilli attended an anecdote about his life:It turned out that, about 10 years later, Ciro ended up following this advice, unwittingly.
I used to want to learn Mathematics.But it was very hard.So in the end, I became an engineer, and found an engineering solution to the problem, and married a Mathematician instead.
Ciro once read that there are two types of mathematicians/scientists (he thinks it was comparing Einstein to some Jack of all trades polymath who didn't do any new discoveries):
- high flying birds, who know a bit of everything, feel the beauty of each field, but never dig deep in any of them
- gophers, who dig all the way down, on a single subject, until they either get the Nobel Prize, or work on the wrong problem and waste their lives
TODO long after Ciro forgot where he had read this from originally, someone later pointed him to: www.ams.org/notices/200902/rtx090200212p.pdf Birds and Frogs by Freeman Dyson (2009), which is analogous but about Birds and Frogs. So did Ciro's memory play a trick on him, or is there also a variant; of this metaphor with a gopher?
Ciro is without a doubt the bird type. Perhaps the ultimate scientist is the one who can combine both aspects in the right amount?
Ciro gets bored of things very quickly.
Once he understands the general principles, if the thing is not the next big thing, Ciro considers himself satisfied without all the nitty gritty detail, and moves on to the next attempt.
In the field of mathematics for example, Ciro is generally content with understanding cool theorem statements. More generally, one of Ciro's desires is for example to understand the significance of each physics Nobel Prize.
This is also very clear for example after Ciro achieved Linux Kernel Module Cheat: he now had the perfect setup to learn all the Linux kernel shady details but at the same time after all those years he finally felt that "he could do it, so that was enough", and soon moved to other projects.
If Ciro had become a scientist, he would write the best review papers ever, just like in the current reality he writes amazing programming tutorials on Stack Overflow.
Ciro has in his mind an overly large list of subjects that "he feels he should know the basics of", and whenever he finds something in one of those topics that he does not know enough about, he uncontrollably learns it, even if it is not the most urgent thing to be done. Or at least he puts a mention on his "list of sources" about the subject. Maybe everyone is like that. But Ciro feels that he feels this urge particularly strongly. Correspondingly, if a subject is not in that list, Ciro ignores it without thinking twice.
Ciro believes that high flying birds are the type of people better suited for venture capital investment management: you know a bit of what is hot on several fields to enough depth to decide where to place your bets and how to guide them. But you don't have the patience to actually go deeply into any one of them and deal with each individual shit that comes up.
Cosmos: A Personal Voyage (1980) episode 1 mentions as quoted by the Wikipedia page for Eratosthenes:That's Ciro.
According to an entry in the Suda (a 10th-century encyclopedia), his critics scorned him, calling him beta (the second letter of the Greek alphabet) because he always came in second in all his endeavours.
Some related ideas:
This dude looks like a God. Ciro Santilli does not understand his stuff, but just based on the names of his theories, e.g. "Yoga of anabelian algebraic geometry", and on his eccentric lifestyle, it is obvious that he was in fact a God.
Good film about him: Blaise Pascal (1972).
Good quote from his Les Provinciales (1656-57) Letter XII, p. 227:French version reproduced at: www.dicocitations.com/citation/auteurajout35106.php.
The war in which violence endeavors to crush truth is a strange and a long one.All the efforts of violence cannot weaken truth, but only serve to exalt it the more.The light of truth can do nothing to arrest violence; nay, it serves to provoke it still more.When force opposes force, the more powerful destroys the less; when words are opposed to words, those which are true and convincing destroy and scatter those which are vain and false; but violence and truth can do nothing against each other.Yet, let no one imagine that things are equal between them; for there is this final difference, that the course of violence is limited by the ordinance of God, who directs its workings to the glory of the truth, which it attacks; whereas truth subsists eternally, and triumphs finally over its enemies, because it is eternal, and powerful, like God Himself.
A way to defined geometry without talking about coordinates, i.e. like Euclid's Elements, notably Euclid's postulates, as opposed to Descartes's Real coordinate space.
Postulates are what we now call axioms.
There are 5: en.wikipedia.org/w/index.php?title=Euclidean_geometry&oldid=1036511366#Axioms, the parallel postulate being the most controversial/interesting.
With major mathematicians holding ideas such as:it is not surprise that the state of STEM education is so shit as of 2020, especially at the the missing link between basic and advanced! This also implies that the number of people that can appreciate any advanced mathematics research is tiny, and consequently so is the funding.
Exposition, criticism, appreciation, is work for second-rate minds. [...] It is a melancholy experience for a professional mathematician to find himself writing about mathematics. The function of a mathematician is to do something, to prove new theorems, to add to mathematics, and not to talk about what he or other mathematicians have done.
Works on percolation theory.
Ciro Santilli's wife, who was frustrated with academia at some point, admires the fact that Simons managed to make infinite money, and then invested back in actual science, e.g. through the Simons Foundation.
Jim Simons in 2007
. Tagged
The cool think about Ramanujan is how British mathematicians heard about him and then just went crazy that someone they had never heard of before had come up with so many novel results. It is as if God had come down from the clouds and handed them those results. Without proof. But in that field of research, the statements are not easy to come up with, so much so that G. H. Hardy commented that:
they must be true, because, if they were not true, no one would have the imagination to invent them
The man who loved numbers by WGBH
. Source. Season 15 Episode 19 from their series Nova (1988)The cool thing about Terrence Tao is that besides being a mathematical genius, he is also interested in modern technology such as formal proof systems and automated theorem proving. For that, kudos.
It is hard to decide what makes Ciro Santilli more sad: the usage of Greek letters, the invention of new symbols, or the fifty million alternative font styles used.
Only Chinese characters could be worse than that!
These are not in the Greek alphabet:
By Evan Chen.
800+ page PDF with source on GitHub claiming to try and teach the beauty of modern maths for high schoolers. Fantastic project!!!
Author of Infinite Napkin.
He's also a mathematical olympiad coach.
v3 LaTeX source code: github.com/OperaMagistris/Opera_Magistris_English_v3
Very unfortunate license "public domain license" with a "non religious" clause, whatever the fuck that is, which completely defeats the point of a public domain declaration:
The source code and text is under Public License and therefore can be used, translated and distributed at free will.It is only banned to use the text and content for religious propaganda.
- Renders: stacks.math.columbia.edu/. HTML is one tiny section per page, making it unreadable.
- LaTeX source: github.com/stacks/stacks-project
The book is very dry, extremelly boring unfortunately. Definition and theorem only for the most part.
When you see some tagged examples, you will immediately know what this means.
Tagged
Amazing graphs and formulas.
Python graphics engine open sourced at: github.com/3b1b/manim "Animation engine for explanatory math videos". But for some reason there is a community fork: github.com/ManimCommunity/manim/ "This repository is maintained by the Manim Community, and is not associated with Grant Sanderson or 3Blue1Brown in any way (though we are definitely indebted to him for providing his work to the world). If you want to study how Grant makes his videos, head over to his repository (3b1b/manim). This is a more frequently updated repository than that one, and is recommended if you want to use Manim for your own projects." what a mess.
He got so old from 2012 to 2021 :-)
This dude did well. If only he had written a hyperlinked wiki rather than making videos! It would allow people to jump in at any point and just click back. It would be Godlike.
mathdoctorbob.org/About.html says:
Robert Donley received his doctorate in Mathematics from Stony Brook University and has over two decades of teaching experience at the high school, undergraduate, and graduate levels.
Ancestors
Incoming links
- Home
- Adolfo Amidei
- Art
- The best articles by Ciro Santilli
- Ciro Santilli's bad old event memory
- Classification (mathematics)
- Computer science
- Deletionism on Wikipedia
- Eli Benderski
- Existence and uniqueness
- Fields Medal
- High budget movies are shit
- High flying bird vs gophers
- High-frequency trading as a form of Nirvana
- Infinity
- Magic: The Gathering
- Marco Troper
- Mathematics
- Mathematics illustration software
- Minimal working example
- Molecular Sciences Course of the University of São Paulo
- Numerical analysis
- OurBigBook.com
- Existing data sources
- Physics
- Quantum electrodynamics
- Lecture 2
- Settheory.net
- Why you should give money to Ciro Santilli
- The beauty of mathematics
- The perfect video game is an infinitely hard one
- There is value in tutorials written by early pioneers of the field
- Website front-end for a mathematical formal proof system
- Wikipedia CatTree