Statistical physics

Theory that gases are made up of a bunch of small billiard balls that don't interact with each other.

This theory attempts to deduce/explain properties of matter such as the equation of state in terms of classical mechanics.

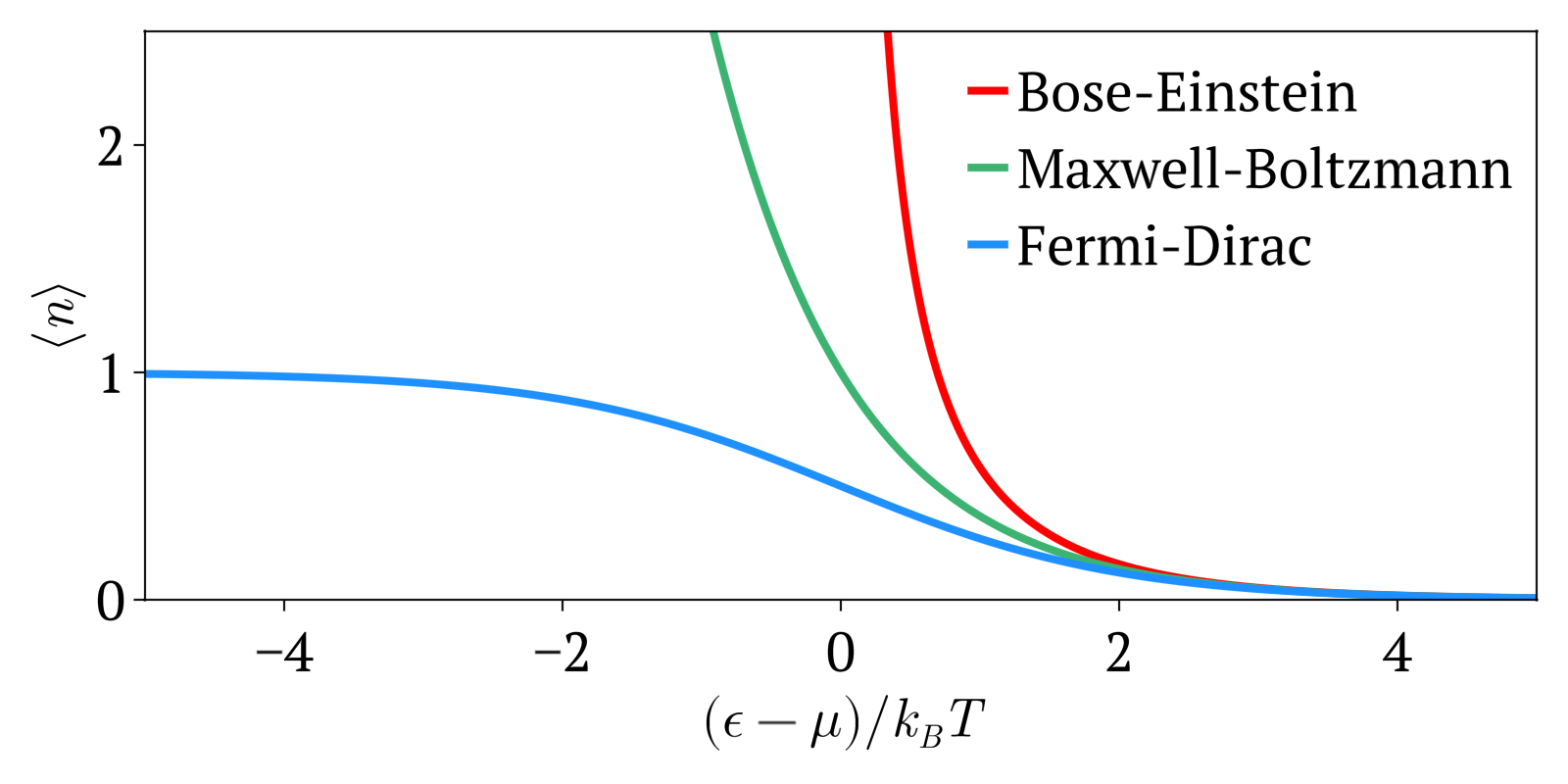
Maxwell-Boltzmann statistics, Bose-Einstein statistics and Fermi-Dirac statistics all describe how energy is distributed in different physical systems at a given temperature.

For example, Maxwell-Boltzmann statistics describes how the speeds of particles are distributed in an ideal gas.

The temperature of a gas is only a statistical average of the total energy of the gas. But at a given temperature, not all particles have the exact same speed as the average: some are higher and others lower than the average.

For a large number of particles however, the fraction of particles that will have a given speed at a given temperature is highly deterministic, and it is this that the distributions determine.

One of the main interest of learning those statistics is determining the probability, and therefore average speed, at which some event that requires a minimum energy to happen happens. For example, for a chemical reaction to happen, both input molecules need a certain speed to overcome the potential barrier of the reaction. Therefore, if we know how many particles have energy above some threshold, then we can estimate the speed of the reaction at a given temperature.

The three distributions can be summarized as:

A good conceptual starting point is to like the example that is mentioned at The Harvest of a Century by Siegmund Brandt (2008).

Consider a system with 2 particles and 3 states. Remember that:

Therefore, all the possible way to put those two particles in three states are for:

Most applications of the Maxwell-Boltzmann distribution confirm the theory, but don't give a very direct proof of its curve.

Here we will try to gather some that do.

Measured particle speeds with a rotation barrel! OMG, pre electromagnetism equipment?

Is it the same as Zartman Ko experiment? TODO find the relevant papers.

edisciplinas.usp.br/pluginfile.php/48089/course/section/16461/qsp_chapter7-boltzman.pdf mentions

Start by looking at: Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics.

Start by looking at: Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics.

Bibliography:

This is not a truly "fundamental" constant of nature like say the speed of light or the Planck constant.

Rather, it is just a definition of our Kelvin temperature scale, linking average microscopic energy to our macroscopic temperature scale.

The way to think about that link is, at 1 Kelvin, each particle has average energy:per degree of freedom.

This is why the units of the Boltzmann constant are Joules per Kelvin.

For an ideal monatomic gas, say helium, there are 3 degrees of freedom. so each helium atom has average energy:

If we have 2 atoms at 1 K, they will have average energy $6/2k_{B}J$, and so on.

Another conclusion is that this defines temperature as being proportional to the total energy. E.g. if we had 1 helium atom at 2 K then we would have about $6/2k_{B}J$ energy, 3 K $9/2k_{B}J$ and so on.

This energy is of course just an average: some particles have more, and others less, following the Maxwell-Boltzmann distribution.

chemistry.stackexchange.com/questions/7696/how-do-i-distinguish-between-internal-energy-and-enthalpy/7700#7700 has a good insight:

Adds up chemical energy and kinetic energy.

Wikipedia mentions however that the kinetic energy is often negligible, even for gases.

The sum is of interest when thinking about reactions because chemical reactions can change the number of molecules involved, and therefore the pressure.

To predict if a reaction is spontaneous or not, negative enthalpy is not enough, we must also consider entropy via Gibbs free energy.

Bibliography:

TODO understand more intuitively how that determines if a reaction happens or not.

At least from the formula we see that:

A prototypical example of reaction that is exothermic but does not happen at any temperature is combustion.

I think these are the ones where $\Delta H\times \Delta S>0$, i.e. enthalpy and entropy push the reaction in different directions. And so we can use temperature to move the Chemical equilibrium back and forward.

OK, can someone please just stop the philosophy and give numerical predictions of how entropy helps you predict the future?

The original notion of entropy, and the first one you should study, is the Clausius entropy.

For entropy in chemistry see: entropy of a chemical reaction.

TODO why it is optimal: physics.stackexchange.com/questions/149214/why-is-the-carnot-engine-the-most-efficient

Subtle is the Lord by Abraham Pais (1982) chapter 4 "Entropy and Probability" mentions well how Boltzmann first thought that the second law was an actual base physical law of the universe while he was calculating numerical stuff for it, including as late as 1872.

But then he saw an argument by Johann Joseph Loschmidt that given the time reversibility of classical mechanics, and because they were thinking of atoms as classical balls as in the kinetic theory of gases, then there always exist a valid physical state where entropy decreases, by just reversing the direction of time and all particle speeds.

So from this he understood that the second law can only be probabilistic, and not a fundamental law of physics, which he published clearly in 1877.

Considering e.g. Newton's laws of motion, you take a system that is a function of time $f(t)$, e.g. the position of many point particles, and then you reverse the speeds of all particles, then $f(-t)$ is a solution to that.

I guess you also have to change the sign of the gravitational constant?

TODO can anything interesting and deep be said about "why phase transition happens?" physics.stackexchange.com/questions/29128/what-causes-a-phase-transition on Physics Stack Exchange

Mentioned at: en.wikipedia.org/wiki/Phase_transition#Modern_classifications

The more familiar transitions we are familiar with like liquid water into solid water happen at constant temperature.

However, other types of phase transitions we are less familiar in our daily lives happen across a continuum of such "state variables", notably:

Reaches 2 mK^[ref]. youtu.be/upw9nkjawdy?t=487 from Video "Building a quantum computer with superconducting qubits by Daniel Sank (2019)" mentions that 15 mK are widely available.

Used for example in some times of quantum computers, notably superconducting quantum computers. As mentioned at: youtu.be/uPw9nkJAwDY?t=487, in that case we need to go so low to reduce thermal noise.

Users:

For scales from absolute 0 like Kelvin, is proportional to the total kinetic energy of the material.

The Boltzmann constant tells us how much energy that is, i.e. gives the slope.